সাপ্তাহিক সমস্যা-১৯ এর সমাধান (Problem Weekly–19 with Solution)

Jun 20, 2023 | Problem Weekly (সাপ্তাহিক সমস্যা)

সাপ্তাহিক সমস্যা-১৯: সংখ্যাভাবুক সৌভিক প্রতিদিনের মত আজকে সকালে নিজের খাতায় 1 থেকে 9 পর্যন্ত অঙ্কগুলো ব্যবহার করে বিভিন্ন সংখ্যা তৈরী করছে।  হঠাৎ করে সৌভিক একটা মজার বিষয় লক্ষ করলো; সে নিজের খাতায় তিনটি সংখ্যা লিখেছে এবং এই তিনটি সংখ্যার মধ্যে সবথেকে বড় সংখ্যাটি হল সবচেয়ে ছোট সংখ্যার পাঁচগুণ! আর অপর যে সংখ্যাটি রয়েছে, সেটি সবচেয়ে ছোট সংখ্যাটির তিনগুণ!
সহজে বোঝার সুবিধার্থে বলা যায়, যদি তিনটি সংখ্যা যথাক্রমে a, b, c হয় যেখানে a> b> c, তাহলে, a:b:c = 5:3:1 লিখা যায়। শুধুমাত্র ১ থেকে ৯ – এই নয়টি অঙ্ক একবার করে ব্যবহার করে সৌভিক সংখ্যা তিনটি লিখেছে।
আচ্ছা, তোমরা কি সৌভিকের এই তিনটি সংখ্যা বের করতে পারবে?

Problem Weekly-19: Number-lover Souvik makes different numbers by using the digits from 1 to 9 in his notebook like every day. Suddenly Sauvik noticed something interesting; he wrote three numbers in his notebook. Interestingly, among these three numbers, the largest is five times the smallest. And the other number is three times the smallest number!
To explain the statement clearly, let’s say if three numbers are a, b, and c respectively where a> b> c, then we can say a:b:c = 5:3:1. Using the nine digits from 1 to 9 only once, Sauvik writes these three numbers.
Well, can you figure out these three numbers?

সমাধান: যেহেতু,  a:b:c = 5:3:1 বা a সংখ্যাটি হবে c সংখ্যার পাঁচগুণ, b সংখ্যাটি হবে c সংখ্যার তিনগুণ, এবং ১ থেকে ৯ অঙ্কগুলো একবার করে ব্যবহৃত হয়েছে,  

তাহলে আমরা বলতে পারি যে, c সংখ্যাটি এক অঙ্ক বা দুই অঙ্কের হতে পারবে না, অন্তত তিন অঙ্কের হতে হবে। কারণ c যদি এক অঙ্ক বা দুই অঙ্কের হয়, সেক্ষেত্রে b কিংবা a সর্বোচ্চ তিন অঙ্কের হবে, তখন ৮টি অঙ্কের বেশি ব্যবহার করার সুযোগ থাকবে না। এছাড়া c সংখ্যাটি তিন অঙ্কের বেশিও হতে পারবে না, সেক্ষেত্রে আমাদের শর্ত ভঙ্গ হবে! 

তাহলে আমরা নিশ্চিত যে, c সংখ্যাটি তিন অঙ্কের হবে। এখন c এর শতক স্থানীয় অঙ্কে 1 অঙ্কটি বসাতে হবে, শতক স্থানীয় অঙ্কে 1 বাদে কোন অঙ্ক বসলে বৃহত্তম সংখ্যা a চার অঙ্ক বিশিষ্ট সংখ্যায় পরিণত হবে যা শর্ত ভঙ্গ করে! আবার, c এর একক স্থানীয় অঙ্কে কোন জোড় অঙ্ক বসতে পারবে না, কেননা জোড় সংখ্যা বসলে a সংখ্যাটির একক স্থানীয় অঙ্কটিকে ০ হতে হবে যা প্রদত্ত শর্তের বাইরে।

একইভাবে, c এর একক স্থানীয় অঙ্কে 5 বসতে পারবে না, কেননা  a এর একক স্থানীয় অঙ্ক সেক্ষেত্রে 5 হবে যা সম্ভব না। (কেন বলো তো!)

একই নিয়মে, c এর একক স্থানীয় অঙ্কে 7 বসতে পারবে না, কেননা b এর একক স্থানীয় অঙ্ক 1 হতে পারবে না!

তাহলে বলা যায়, c এর একক স্থানীয় অঙ্কে হয় 3 অথবা 9 অঙ্কটি বসবে।

যদি c এর একক স্থানীয় অঙ্ক 3 হয়, তাহলে b এর একক স্থানীয় অঙ্ক 9 হবে এবং a এর একক স্থানীয় অঙ্ক হবে 5।

আবার, b এর শতক স্থানীয় অঙ্ককে অবশ্যই 3, 4 কিংবা 5 হতে হবে কেননা c এর শতক স্থানীয় অঙ্ক 1।

আগের শর্ত থেকে, যদি c এর একক স্থানীয় অঙ্ক 3 হয়, তাহলে b এর শতক স্থানীয় অঙ্ককে 4 হতে হবে। (ভেবে দেখো কেন এটা হবে!)

সেক্ষেত্রে আমরা যে অঙ্কগুলো ব্যবহার করেছি সেগুলো হলো 1, 3, 4,  5, 9।  বাকি অংকগুলো হলো- 2, 6, 7, 8।

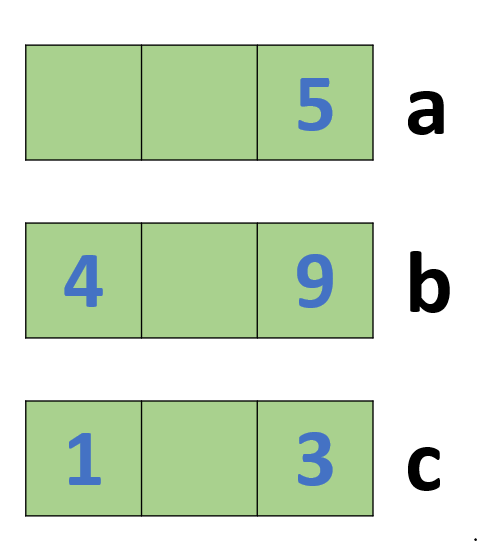
ছবি: c সংখ্যার জন্য় এককের ঘরে 3 অঙ্কটি বসেছে

এখন c এর দশক স্থানীয় অঙ্ক হিসেবে যে অঙ্কগুলো বসতে পারে সেগুলো হলো- 2, 6, 7, 8। কিন্তু এদের কোনোটাই বসতে পারবে না! কারণ c এর দশক স্থানীয় অঙ্ক 2 বা 6 বা 7 বা 8 হলে b এর শতক স্থানীয় অঙ্ক হিসেবে 4 কোনোভাবেই বসতে পারবে না এবং প্রতিবারই এই অঙ্কগুলোর জন্য বাকি সংখ্যাতে একই অঙ্ক একাধিকবার চলে আসে কিংবা ১-৯ পর্যন্ত সবগুলো অঙ্ক একবার করে ব্যবহারের সুযোগ থাকে না। অর্থাৎ, c এর একক স্থানীয় অঙ্কে 3 বসানো যাবে না।

তাহলে, c এর একক স্থানীয় জায়গায় ৯ অঙ্কটিই বসবে! সেক্ষেত্রে, b এর একক স্থানীয় অঙ্কে 7 বসবে এবং a সংখ্যাটির একক স্থানীয় অঙ্কে 5 বসবে।

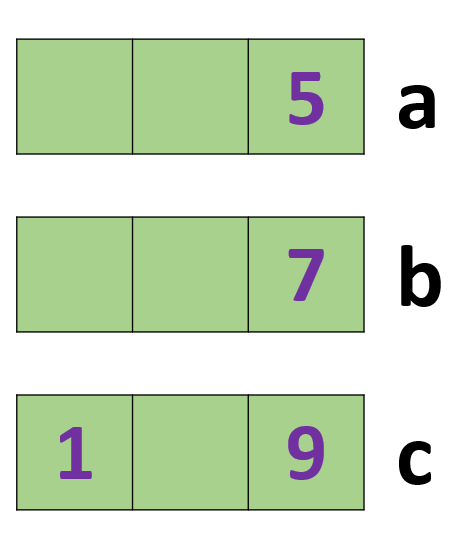
ছবি: c সংখ্যার জন্য় এককের ঘরে 9 অঙ্কটি বসেছে

কিন্তু আমরা শুধুমাত্র c এর দশক স্থানীয় অঙ্কে 2 বসিয়ে সমাধান পাবো, বাকি অঙ্কগুলোর জন্য সমাধান আসবে না, কোন না কোন শর্ত অমান্য হবেই।
(তুমি চাইলে হিসেব করে দেখতে পারো আমাদের উত্তর ঠিক না ভুল হয়েছে!)

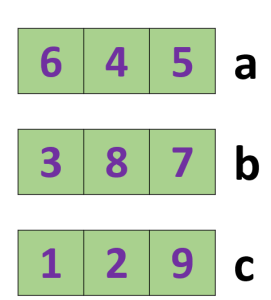
ছবি: c, b এবং a সংখ্যা তিনটির সঠিক মান

সুতরাং, c এর মান হবে 129, b এর মান হবে 387, এবং a এর মান হবে 645 । এটাই আমাদের এই এই সপ্তাহের গাণিতিক সমস্যার উত্তর!

অনেকেই আমাদের কাছে এই গাণিতিক সমস্যাটির সমাধান পাঠিয়েছে, সবার স্বতঃস্ফূর্ত অংশগ্রহণ আমাদের অভিভূত করেছে। শুধুমাত্র ১ জনের সঠিক উত্তর পেয়েছি, তাই সাপ্তাহিক সমস্যা-১৯ এ আমাদের বিজয়ী ১ জন!

ছবি: সাপ্তাহিক সমস্যা-১৯ এর বিজয়ী তালিকা

যারা উত্তর পাঠিয়েছেন, সবাইকে অভিনন্দন। আশা করি আপনাদের সমস্যা সমাধানের এই যাত্রা অব্যাহত থাকবে। সবার সেকেন্ড ডিফারেন্সিয়াল নেগেটিভ হোক!

(আমাদের অন্যান্য গাণিতিক সমস্যা দেখতে এই লিঙ্কে ক্লিক করুন।) 

সাপ্তাহিক সমস্যা-১৮ এর সমাধান (Problem Weekly–18 with Solution)

Jun 13, 2023 | Problem Weekly (সাপ্তাহিক সমস্যা)

সাপ্তাহিক সমস্যা-১৮: সংখ্যাভাবুক সৌভিক প্রতিদিনের মত নিজের খাতায় বিভিন্ন সংখ্যা লিখে চিন্তা-ভাবনা করছে। আজকে সে মৌলিক সংখ্যার যে লুকায়িত সৌন্দর্য আছে, সেটি নিয়ে ভাবছে। মৌলিক সংখ্যা হলো সেসব সংখ্যা যাদেরকে শুধুমাত্র 1 এবং ঐ সংখ্যা দ্বারা ভাগ করা যায়। যেমন: 3, 5, 11 ইত্যাদি। মৌলিক সংখ্যা নিয়ে কিছু মজার তথ্য আছে যেমন: 2 একমাত্র জোড় মৌলিক সংখ্যা, সবচেয়ে বড় মৌলিক সংখ্যা নিশ্চিত করে বলা যায় না, টেলিযোগাযোগ প্রযুক্তিতে মৌলিক সংখ্যা ব্যবহার করা হয় ইত্যাদি।

যাই হোক, সৌভিক চিন্তা করতে করতে খাতায় দুইটি মৌলিক সংখ্যা লিখলো। সে তখন মজার একটা ব্যাপার লক্ষ করলো। বোঝার সুবিধার্থে ধরা যাক, সৌভিক খাতায় a, b দুইটি মৌলিক সংখ্যা লিখেছে। মজার ব্যাপার, a+b ও একটি মৌলিক সংখ্যা, 2a-1 এবং 2b-1 এই দুইটি রাশিও মৌলিক সংখ্যা! অর্থাৎ a, b, a+b, 2b-1, 2a-1 এই পাঁচটিই মৌলিক সংখ্যা। আচ্ছা বলতো, এরকম বৈশিষ্ট্য সৌভিক কয়বার দেখতে পারবে? উত্তরের স্বপক্ষে ভালো যুক্তি দিতে হবে কিন্তু!

Problem Weekly-18:Number-lover Souvik is thinking about different numbers as usual. Today he is thinking about the hidden beauty of prime numbers. Prime numbers are those numbers that can only be divided by 1, and that number. For example 3, 5, 11, etc. Some properties of prime numbers are such as 2 is the only even prime number, and the largest prime number cannot be said with certainty, these numbers are used in the telecommunication sector, etc.

Souvik noticed an interesting fact when he wrote two prime numbers in his notebook. For understanding, let’s say that Souvik writes two prime numbers a,b in his notebook. An interesting fact is that a+b is a prime number, and 2a-1 and 2b-1 are also prime numbers. It means a, b, a+b, 2b-1, 2a-1  all five are prime numbers. Well, how many times can Souvik see such an incident? You must answer with strong logic in favor of your statement!

সমাধান: শর্তমতে, a, b, a+b, 2b-1, 2a-1 এই পাঁচটি সংখ্যাই মৌলিক সংখ্যা হতে হবে।

এখন a, b এই দুইটি যদি বিজোড় সংখ্যা হয়, তাহলে a+b অবশ্যই জোড় সংখ্যা হতে হবে।

কিন্তু a+b জোড় মৌলিক সংখ্যা হলে a+b = 2 হতে হবে যেটা অসম্ভব!

তাহলে বলা যায়, a, b এর মধ্যে একটি জোড় এবং একটি বিজোড় মৌলিক সংখ্যা হতে হবে। এর মানে একটির মান হবে 2।

ধরি, a = 2

তাহলে, 2a – 1 = 2*2 – 1 = 3 যা একটি মৌলিক সংখ্যা।

এবার আমাদেরকে b এর এমন একটি মান বের করতে হবে যেন b, b+2, 2b-1 এই তিনটি সংখ্যাই মৌলিক হয়।

যেহেতু b একটি বিজোড় সংখ্যা এবং b, b+2 দুইটি ক্রমিক বিজোড় সংখ্যা, তাহলে ধরে নিই, b এর মান 3 এর চেয়ে বেশী।

এখান থেকে আমরা বলতে পারি, b কে 6 দিয়ে ভাগ করলে ভাগশেষ 5 থাকবে এবং b+2 কে 6 দিয়ে ভাগ করলে ভাগশেষ 1 থাকবে।

অর্থাৎ, b কে আমরা 6k-1 আকারে লিখতে পারবো।

[ নোট: 2 এবং 3 বাদে যে কোনো বিজোড় মৌলিক সংখ্যাকে 6k+1 বা 6k-1 আকারে লেখা যায়। যেমন: 11 = 6*2-1, 43 = 6*7+1 ইত্যাদি ]

যদি b = 6k-1 হয়, তাহলে 2b-1 কে আমরা লিখতে পারি-

2b-1 = 2(6k-1) -1 = 12k-2-1= 12k-3 =3(4k-1)

অর্থাৎ আমরা বলতে পারি, 2b-1 সংখ্যাটি 3 দ্বারা বিভাজ্য হবে যদি b এর মান 3 এর চেয়ে বড় হয়।

যদি b এর মান 3 হয় তাহলে-

a=2, যা একটি মৌলিক সংখ্যা

b=3, যা একটি মৌলিক সংখ্যা

2b-1 = 2*3-1 = 5, যা একটি মৌলিক সংখ্যা

a+b = 2+3 = 5, যা একটি মৌলিক সংখ্যা

2a-1 = 2*2-1 = 3, যা একটি মৌলিক সংখ্যা

সুতরাং, a = 2 এবং b = 3 অথবা a = 3 এবং b = 2 এটি দুইটিই সম্ভব্য সমাধান।

অনেকেই আমাদের কাছে এই গাণিতিক সমস্যাটির সমাধান পাঠিয়েছে, সবার স্বতঃস্ফূর্ত অংশগ্রহণ আমাদের অভিভূত করেছে। মোট ২ জনের সঠিক উত্তর পেয়েছি আমরা, তাই সাপ্তাহিক সমস্যা-১৮ এ আমাদের মোট বিজয়ী ২ জন!

ছবি: সাপ্তাহিক সমস্যা-১৮ এর বিজয়ীদের তালিকা

যারা উত্তর পাঠিয়েছেন, সবাইকে অভিনন্দন। আশা করি আপনাদের সমস্যা সমাধানের এই যাত্রা অব্যাহত থাকবে। সবার সেকেন্ড ডিফারেন্সিয়াল নেগেটিভ হোক!

(আমাদের অন্যান্য গাণিতিক সমস্যা দেখতে এই লিঙ্কে ক্লিক করুন।) 

সাপ্তাহিক সমস্যা-১৭ এর সমাধান (Problem Weekly–17 with Solution)

Jun 7, 2023 | Problem Weekly (সাপ্তাহিক সমস্যা)

সাপ্তাহিক সমস্যা-১৭: সংখ্যাভাবুক সৌভিক প্রতিদিনের মত আজকে সকালেও সংখ্যা নিয়ে চিন্তা করছিলো। সে সকাল থেকে সংখ্যাতত্ত্বের একটি বই পড়ছে। বই পড়ার এক পর্যায়ে সে দেখলো, Cryptarithmetic নামে গণিতে একটি শাখা আছে। যেমন- সংখ্যাকে তো আমরা বিভিন্ন ভাষায় লিখে থাকি; 10 কে আমরা বাংলায় দশ বা ইংরেজিতে TEN হিসেবে লিখি। মজার ব্যাপার হলো, গণিতের Cryptarithmetic শাখায় সংখ্যাকে অন্য ভাষার বিভিন্ন অক্ষর দিয়ে প্রকাশ করা হয়। Cryptarithmetic এ সংখ্যাকে বিভিন্ন বর্ণ দিয়ে প্রকাশ করা হয় এবং প্রতিটি বর্ণ আলাদা আলাদা অঙ্ককে নির্দেশ করে থাকে। সৌভিক সাথে সাথেই Cryptarithmetic নিয়ে গাণিতিক সমস্যা চিন্তা করতে লাগলো। কিছুক্ষণ পর সে একটি সমস্যা খুঁজে পেল যা উপরের ছবিতে দ্রষ্টব্য। তোমরা কি সৌভিকের দেয়া সমস্যাটি সমাধান করতে পারবে?

Problem Weekly-17: Number-lover Souvik has been thinking about numbers since this morning as usual. He is reading an interesting book on Number-theory. At one stage of reading the book, he finds that there is a branch of mathematics called Cryptarithmetic. Well, we can write numbers in different languages, just for numeric 10, we write ‘দশ’ in Bangla or ‘TEN’ in English. Interestingly, in the cryptarithmetic branch, numbers are written using letters in other languages, and each letter represents a different digit. Souvik immediately starts thinking about a cryptarithmetic problem. After a while, he found a problem that is given in the above picture. Well, can you solve the problem given by Souvik?

সমাধান: আমাদের সমস্যাটি হলো এরকম-

  FORTY
      TEN
+   TEN
————-
  SIXTY 

আমরা যদি একক স্থানীয় অঙ্কের দিকে লক্ষ করি,

Y+ N+ N = Y

এখান থেকে আমরা বলতে পারি,  N এর মান শুন্য কিংবা পাঁচ হতে পারে। এখন যদি N এর মান 5 হয় তাহলে,

দশক স্থানীয় অঙ্কের ক্ষেত্রে আমরা পাই,  T+E+E+1 (একক স্থানীয় অংকের জন্য হাতে রাখা 1) = T  যা অসম্ভব!

তাহলে আমরা নিশ্চিত হয়ে বলতে পারি,

N= 0

যেহেতু প্রতিটি বর্ণ আলাদা আলাদা অঙ্ককে নির্দেশ করে, তাই নিশ্চিত করে বলতে পারি  E এর মান হবে 5।

S এবং F যেহেতু ভিন্ন ভিন্ন অঙ্ককে নির্দেশ করবে (কেন বলো তো!), একইভাবে O এবং I যেহেতু ভিন্ন ভিন্ন অঙ্ককে নির্দেশ করবে, তাহলে লিখা যায়-

S = F+1 ………….(i)

I = O+1 অথবা I = O+2 (আচ্ছা, I = O+3 কেন হবে না?) ………….(2)

এবং শতক এর অঙ্ক হিসেবে লিখা যায়,

R+T+T+1 = X+10P (p=1 অথবা p=2 হতে পারে) ……….(3)

আচ্ছা, সমীকরণ দেখে কিছু বুঝতে পারছো কী? যেমন দেখো, তিনটি এক অঙ্কের সংখ্যার যোগফল কখনো 27 এর বেশী হতে পারে না! এজন্য আমরা সমীকরণ (3) এর ক্ষেত্রে বলেছি যে, P এর মান 3 হতে পারবে না।

যদি P = 1 হয়, তাহলে আমরা শতক স্থানীয় অঙ্কগুলো যোগ করে পাই,

R+T+T+1 = X+10

এর মানে এখান থেকে আমরা 1 হাতে রাখতে পারবো বা carry হিসেবে 1 থাকবে। অর্থাৎ,

I = O+1, বা, O = 9 এবং I = 0 হয়

কিন্তু এটা সম্ভব  না! কারণ N = 0 আমরা আগেই দেখেছি। তাহলে আমরা বুঝতে পারছি যে, P = 2 হবে। তাহলে বলা যায়-

 R+ T+ T+ 1 = X+20 হবে

বা, R+T+T = X+19 হবে

এবং,  I = O+2 হবে যেখানে O = 9 এবং I = 1 হয়।

এখন, যেহেতু R+T+T = X+19 তাহলে আমরা ধরে নিই-

T = 8R = 6X = 3 

তাহলে আমরা লিখতে পারি,

 F968Y
      850
 +  850
———-
 S138Y

যেহেতু F এবং S ক্রমিক বা পাশাপাশি সংখ্যা হবে, সেহেতু T=8, R=6, X=3 হতে পারবে না।

আমরা তাহলে অন্যকিছু ধরে আগাতে পারি। ধরি,  T= 8R= 7X = 4 । তাহলে আমাদের সংখ্যা পাজল এরকম হবে-

 F978Y
    850
+ 850
———
S148Y

তাহলে, F=2 এবং S=3  পাওয়া যায়। সেক্ষেত্রে আমরা বলতে পারি,  Y=6 হবে। তাহলে সমাধানটি হবে এরকম-

29786
     850
+  850
———-
31486

অনেকেই আমাদের কাছে এই গাণিতিক সমস্যাটির সমাধান পাঠিয়েছে, সবার স্বতঃস্ফূর্ত অংশগ্রহণ আমাদের অভিভূত করেছে। মোট ৩ জনের সঠিক উত্তর পেয়েছি আমরা, তাই সাপ্তাহিক সমস্যা-১৭ এ আমাদের মোট বিজয়ী ৩ জন!

ছবি: সাপ্তাহিক সমস্যা-১৭ এর বিজয়ী তালিকা

যারা উত্তর পাঠিয়েছেন, সবাইকে অভিনন্দন। আশা করি আপনাদের সমস্যা সমাধানের এই যাত্রা অব্যাহত থাকবে। সবার সেকেন্ড ডিফারেন্সিয়াল নেগেটিভ হোক!

(আমাদের অন্যান্য গাণিতিক সমস্যা দেখতে এই লিঙ্কে ক্লিক করুন।) 

সাপ্তাহিক সমস্যা-১৬ এর সমাধান (Problem Weekly–16 with Solution)

May 30, 2023 | Problem Weekly (সাপ্তাহিক সমস্যা)

সাপ্তাহিক সমস্যা-১৬: সংখ্যাভাবুক সৌভিক প্রতিদিনের মত আজকে সকাল থেকে বিভিন্ন সংখ্যা নিয়ে চিন্তা করছে। সৌভিক বিভাজ্যতা এবং উৎপাদক নিয়ে আজকে চিন্তা করছে। সে খাতায় বিভিন্ন সংখ্যা এবং তাদের উৎপাদকগুলো বের করে লিখে রাখছে। হঠাৎ করে সে একটা মজার ব্যাপার লক্ষ করলো, সে একটা সংখ্যার মোট ১৬টি উৎপাদক বের করেছে এবং এই ১৬টি উৎপাদকের এককের ঘরের অঙ্কে ০ থেকে ৯ পর্যন্ত সবগুলো অঙ্কই আছে। এরকম বৈশিষ্ট্য অনেক সংখ্যার মধ্যেই থাকতে পারে। সবচেয়ে ছোট এমন কোন সংখ্যা আছে তুমি কি সেটি বের করতে পারবে?
উদাহরণ হিসেবে যদি ১১০ এর কথা চিন্তা করি, ১১০ এর উৎপাদক হিসেব করলে পাওয়া যাবে-  ১, ২, ৫, ১০, ১১, ৫৫, ১১০। এখানে সবগুলো উৎপাদকের শেষের অঙ্কে বা এককের অঙ্কে ০, ১, ২ এবং ৫ অঙ্কটি আছে।

Problem Weekly-16: Number-lover Souvik has been thinking about different numbers since this morning like every day. Souvik is thinking today about divisibility and the factors of numbers. He is writing down different numbers and their factors in this notebook. Suddenly he noticed something interesting. He found a total of 16 factors of a number. And these factors have all the digits 0 to 9 in their unit place or ending with each decimal digit, i.e. 0, 1, 2, … and 9. Such properties can exist in many numbers. Can you find the smallest number?
For example, if we consider the number 110 as an example, then the factors of 110 are 1, 2, 5, 10, 11, 55, 110. All these factors have the digits 0, 1, 2, and 5 in the last digit or in the unit digit.

সমাধান: শুরুতে, আমরা যদি বিভাজ্যতা নিয়ে খুব সহজ কয়েকটি জিনিস প্রয়োগ করি তাহলে সমস্যাটি সমাধান করা সহজ হবে।
যেহেতু আমাদের কাঙ্ক্ষিত পূর্ণসংখ্যার উৎপাদকের মধ্যে একটির শেষে অবশ্যই শুন্য থাকতে হবে, এটা নিশ্চিত করে বলা যায় যে সংখ্যাটি অবশ্যই 10 এর গুণিতক হবে বা 10 দ্বারা বিভাজ্য হবে।

তাহলে, কাঙ্ক্ষিত সংখ্যাটির একটি বৈশিষ্ট্য- সংখ্যাটি 10 এর গুণিতক হবে।

আবার, কাঙ্ক্ষিত পূর্ণসংখ্যাটির উৎপাদকের মধ্যে একটির শেষে অবশ্যই 7 অংকটি থাকতে হবে। তাহলে আমরা বলতে পারি যে, আমাদের কাঙ্ক্ষিত সংখ্যাটি 7 এর গুণিতক হতে পারে কিংবা 7, 14, 17, 21, 27… এই ধরণের সংখ্যা দ্বারা বিভাজ্য হতে পারে। এরকম সংখ্যার তালিকা নিম্নরূপ: 

70, 140, 170, 210, 240, 270, 280, 350, 370, 420…..

আবার, পূর্ণসংখ্যাটির উৎপাদকের মধ্যে একটির শেষে অবশ্যই 3 অংকটি থাকতে হবে। সে অনুযায়ী আমরা বলতে পারি, আমাদের কাঙ্ক্ষিত সংখ্যাটি অবশ্যই 3 কিংবা 13 কিংবা 23 …এই ধরণের সংখ্যা দিয়ে বিভাজ্য হবে। এরকম সংখ্যার তালিকা নিম্নরূপ: 

30, 60, 90, 120, 130, 150, 180, 210, 230, 240, 270, 300…..

উপরের কয়েকটি শর্ত অনুসারে আমাদের কাঙ্ক্ষিত সংখ্যাটি হতে পারে-

210, 270, 420……

এখন 210 এর ক্ষেত্রে আমরা চিন্তা করি। 210 এর উৎপাদকগুলো হলো-

1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105,  210

দেখা যাচ্ছে যে, এখানে এরকম কোন উৎপাদক নেই যার শেষের অঙ্ক 8 কিংবা 9। তাহলে,  210 আমাদের উত্তর হবে না।
আমরা 270 এর উৎপাদক বের করার চেষ্টা করি। সংখ্যাটির উৎপাদকগুলো হল-

1, 2, 3, 5, 6, 9, 10, 15, 18, 27, 30, 45, 54, 90, 135, 270

এখানে খুবই স্পষ্ট যে, 270 এর মোট 16টি উৎপাদক এবং এগুলোর শেষে 0 থেকে শুরু করে 9 পর্যন্ত সব কয়টি অঙ্ক রয়েছে! 

সুতরাং, আমাদের সাপ্তাহিক সমস্যা-১৬ এর উত্তর হবে 270।

আচ্ছা, 270 এর পরবর্তী দুইটি সংখ্যা কত হবে সেটা কী বের করতে পারবে? পারলে ঝটপট আমাদের কমেন্টে জানিয়ে দাও তোমার উত্তর। 

অনেকেই আমাদের কাছে এই গাণিতিক সমস্যাটির সমাধান পাঠিয়েছে, সবার স্বতঃস্ফূর্ত অংশগ্রহণ আমাদের অভিভূত করেছে। মোট ২ জনের সঠিক উত্তর পেয়েছি আমরা, তাই সাপ্তাহিক সমস্যা-১৬ এ আমাদের মোট বিজয়ী ২ জন!

ছবি: সাপ্তাহিক সমস্যা-১৬ এর বিজয়ী তালিকা

যারা উত্তর পাঠিয়েছেন, সবাইকে অভিনন্দন। আশা করি আপনাদের সমস্যা সমাধানের এই যাত্রা অব্যাহত থাকবে। সবার সেকেন্ড ডিফারেন্সিয়াল নেগেটিভ হোক!

(আমাদের অন্যান্য গাণিতিক সমস্যা দেখতে এই লিঙ্কে ক্লিক করুন।)