পর্ব ৪: জুনিয়র ক্যাটাগরিতে ভালো করার উপায়
জুনিয়র ক্যাটাগরি বলতে আসলে ষষ্ঠ থেকে অষ্ঠম শ্রেণির এর মধ্যে অন্তর্গত শিক্ষার্থীদের বুঝায়। এই ক্যাটাগরির শিক্ষার্থীরা প্রথম বারের মত ষষ্ঠ শ্রেণি গণিতের অনেক মজার বিষয়ের সাথে পরিচিতি লাভ করে। যেমন: বীজগণিত, জ্যামিতির উপপাদ্য,পরিমিতি ইত্যাদি। এজন্য, অনেক শিক্ষার্থীরা কিন্তু বুঝে উঠতে পারে না কিভাবে এসব বিষয়ে ভালো ধারণা লাভ করবে। জ্যামিতির উপপাদ্যের ক্ষেত্রে কোনো কিছু প্রমাণ করা যুক্তির মত কাজ করে; আমরা পূর্ববর্তী কিছু উপপাদ্য দিয়ে নতুন কোনো উপপাদ্য প্রমাণ করি কিংবা নতুন কোনো জ্যামিতিক সমস্যা সমাধান করে থাকি।
আমরা ইতোমধ্যে আগের লিখাগুলোতে বলেছি যে, অলিম্পিয়াডের প্রশ্নগুলো সংখ্যাতত্ত্ব, গণনা, বীজগণিত, জ্যামিতি, যুক্তি- মূলত এই পাঁচটি বিষয় থেকেই হয়ে থাকে। প্রাথমিক ক্যাটাগরিতে তুলনায় জুনিয়র ক্যাটগরিতে বীজগণিত সম্পর্কিত বেশী সমস্যা দেখা যায়। আগের বারের মত এবারো জুনিয়র ক্যাটাগরির জন্য আমরা কিছু সমস্যা ও তার সমাধানের উপায় নিয়ে আলোচনা করবো।
সংখ্যাতত্ত্ব: সংখ্যার বেলার বিভিন্ন ধরণের সংখ্যা যেমন মৌলিক সংখ্যা , যৌগিক সংখ্যা কিংবা বিভাজ্যতা বা ভাগশেষ এই বিষয়গুলো অনেক গুরুত্বপূর্ন। এরপর গড়, ঐকিক নিয়ম ,শতকরা, লাভ ক্ষতি এই ধরণের গাণিতিক ধারণা থেকেও সমস্যা দেখা যায়। এছাড়া প্যাটার্ন এবং সিরিজ এর বিষয়টি গুরুত্বপূর্ণ।
যেমন নিচের এই সমস্যাটি দেখা যাক-
এই সমস্যা সমাধানের অনেক উপায় বা টেকনিক রয়েছে। গণিত অলিম্পিয়াডে অনেকের যে ব্যাপার নতুন করে জেনে থাকে সেটা হলো Modular arithmatic বা mod। তবে আমরা এখানে আলোচনা করবো কিভাবে একজন শিক্ষার্থী যে কোনো সমস্যাকে ক্ষুদ্র আকারে চিন্তা করতে পারে এবং সমস্যার ভিতরে বিভিন্ন প্যাটার্ন খুঁজে পেতে পারে। যেমন কয়েকটা উদাহরণ দেখি আমরা-
এখানে আমরা 7 এর সূচক এর প্রথম 12 টার মান উল্লেখ করেছি। আচ্ছা, এই বিশাল সংখ্যার মধ্যে কি কোনো প্যাটার্ন বা যোগসূত্র খুঁজে পাওয়া যায়? আচ্ছা, কেনই বা আমরা চারটি চারটি করে আলাদা লিখলাম সংখ্যাগুলোকে? তোমরা কি কিছু বুঝতে পেরেছো? চিন্তা করে দেখো তো!
আচ্ছা, বিভাজ্যতা নিয়ে এই সমস্যাটি দেখা যাক-
𝟑 _ _ 𝟕𝟒 একটি পাঁচ অংকের সংখ্যা যা কিনা 99 দ্বারা বিভাজ্য। তাহলে সংখ্যাটি কত?
𝟑 _ _ 𝟕𝟒 is a five-digit number divisible by 𝟗𝟗. What is the number?
একটু খেয়াল করো যে, 11 দ্বারা বিভাজ্য এবং 9 দ্বারা যদি বিভাজ্য হয় তাহলেই কিন্তু সংখ্যাটি 99 দ্বারা বিভাজ্য হবে। আবার, 9 দ্বারা বিভাজ্য হওয়ার শর্ত হলো, সংখ্যাটির অংকগুলোর যোগফল 9 দ্বারা বিভাজ্য হতে হবে।
আচ্ছা, ধরে নিই যে, সংখ্যাটি 3xy74
তাহলে, 9 দ্বারা বিভাজ্য হতে হলে আমরা বলতে পারি 3 + x + y + 7 + 4 এর মান 9 এর গুনিতক হতে হবে।
এখন, 9 এর গুণিতক হলো 9, 18, 27, 36…..
তাহলে, 14 + x + y = 18 বা 27 হতে পারে কিন্তু 36 বা তার বেশি হতে পারবে না!
আবার, 11 দ্বারা বিভজ্য হওয়ার জন্য 3 + y + 4 – (x + 7) = 0 অথবা 11 হবে।
এখান থেকে পাবো, y – x = 0 অথবা 11
তাহলে, y = x বা y = x + 11
এখান থেকে কিন্তু সহজেই y ও x এর মান বের করে ফেলা যাবে। তাই না? ঝটফট বের করে ফেলো তাহলে।
বীজগণিত: বীজগণিতের ক্ষেত্রে দ্বিঘাত সমীকরণ, সহসমীকরণ, উৎপাদকে বিশ্লেষণ বিভিন্ন বীজগাণিতিক রাশির মান নির্ণয় ইত্যাদি টপিকে ভালো ধারণা রাখতে হয়। একটি সমস্যা নিয়ে আলোচনা করা যাক-
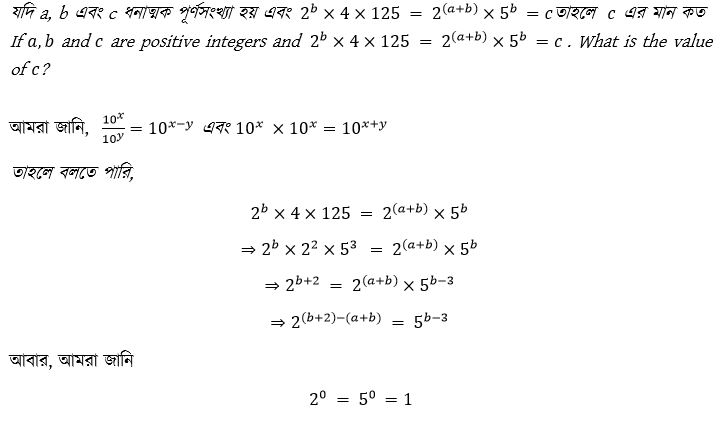 এখান থেকে ধারণা নিয়ে তোমরা তাহলে সমস্যাটি সমাধান করে ফেলো।
এখান থেকে ধারণা নিয়ে তোমরা তাহলে সমস্যাটি সমাধান করে ফেলো।
গণনার ক্ষেত্রে বিন্যাস ও সমাবেশের (Permutation and Combination) প্রাথমিক ধারণা, গণনার যোগজ ও গুণন বিধি যেমন: কতভাবে সাজানো যাবে, কিভাবে সাজানো যাবে এই ধরণের সমস্যা সমাধানের উপায় সম্পর্কে ধারণা থাকতে হবে। এছাড়া, পায়রা খোপ নীতি (Pigeonhole Principle) বিষয়টিও বেশ মজার। যেমন আমরা নিচের সমস্যটি দেখি-
E বর্ণটি GEBON শব্দটি থেকে বাদ দিয়ে দেয়া হলো। বাকি বর্ণগুলি কতগুলি উপায় বিন্যস্ত করা যেতে পারে যাতে O বর্ণটি শুরুতে না থাকে?
The letter E is thrown away from the word GEBON. How many ways can the rest of the letters be jumbled so that O does not appear at the beginning?
এই সমস্যাটিতে মূলত চার বর্ণের একটি শব্দকে কতভাবে সাজানো যেতে পারে সেটি নিয়ে কাজ করতে হবে। 4 টি ভিন্ন ভিন্ন বর্ণ সাজানো যায় 4! উপায়ে। 4! এর মানে হলো 4 × 3 × 2 × 1।
এখন, এই 24 উপায়ের মধ্যে কিছু শব্দ থাকবে যাদের সামনে O বর্নটি থাকবে, সবগুলোতে কিন্তু থাকবে না। আচ্ছা, তোমরা কি এটার উত্তর বের করতে পারবে?
জ্যামিতি: জ্যামিতির জন্য ষষ্ঠ থেকে অষ্ঠম শ্রেণির বইয়ের জ্যামিতির অংশটুকু ভালোমত জানা থাকতে হবে। বিভিন্ন ত্রিভুজ, চতুর্ভুজ, বৃত্তের ক্ষেত্রফল, কোণ সংক্রান্ত বিষয়ের উপর ভালো ধারণা থাকা লাগবে। বিশেষ করে, ত্রিভুজের সর্বসমতা এবং সদৃশতা জানা থাকলে অনেক সমস্যা সমাধানের সহজ হয়ে যায়। আর, পীথাগোরাসের উপপাদ্যটাও বেশ গুরুত্বপূর্ণ।
যেমনপীথাগোরাসের উপপাদ্যের ব্যবহার দিয়ে নিচের সমস্যাটি সমাধান করা যায়-
নিচের চিত্রের সব ত্রিভুজগুলি সমকোণী ত্রিভুজ এবং AB = AC = CD = DE = EF = 1 হয়, তাহলে BF এর মান কত হবে?If all the triangles in the figure are right-angled triangles and AB = CD = DE = EF = 1 , what will be the value of BF?
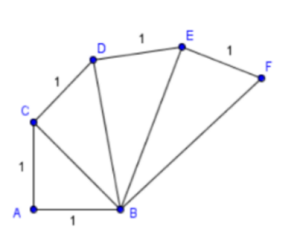
যে কোনো সমকোণী ত্রিভুজের ক্ষেত্রে আমরা জানি, অতিভূজ2 = লম্ব2 + ভূমি2
পাশের ছবি অনুসারে কিন্তু আমরা বলতে পারি, CB2 = AC2 + AB2
এইখান থেকে কিন্তু আমরা CB এর মান যে √2 সেটি খুব সহজেই বলতে পারি। একইভাবে কিন্তু
BD, BE এবং BF এর মান বের করা যায়। ঝটপট তাহলে বের করে ফেলো।
আশা করছি, এই লিখা থেকে জুনিয়র ক্যাটাগরির প্রস্তুতি নিয়ে একটা ভালো ধারণা পাওয়া গেছে। আসলে অলিম্পিয়াডে ভালো করতে হলে বেশি বেশি সমস্যা সমাধানের কোন বিকল্প নেই। আমাদের ওয়েবসাইটে সাপ্তাহিক সমস্যা বিভাগে বিভিন্ন গাণিতিক সমস্যা দেয়া হয়, কেউ চাইলে এগুলো নিয়মিত সমাধান করতে পারে।
পরবর্তী লিখাতে আমরা সেকেন্ডারি ক্যাটাগরির প্রস্তুতি নিয়ে লিখবো। সে পর্যন্ত বাংলার ম্যাথের সাথে থাকুন, গণিতের সাথে থাকুন।
(গণিত অলিম্পিয়াড সিরিজের পর্ব-১ পড়তে এখানে ক্লিক করুন, পর্ব-২ পড়তে এখানে ক্লিক করুন)

