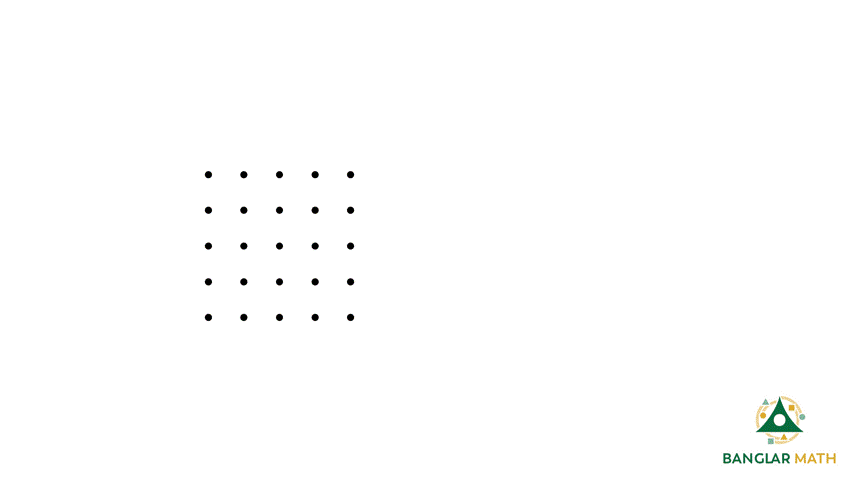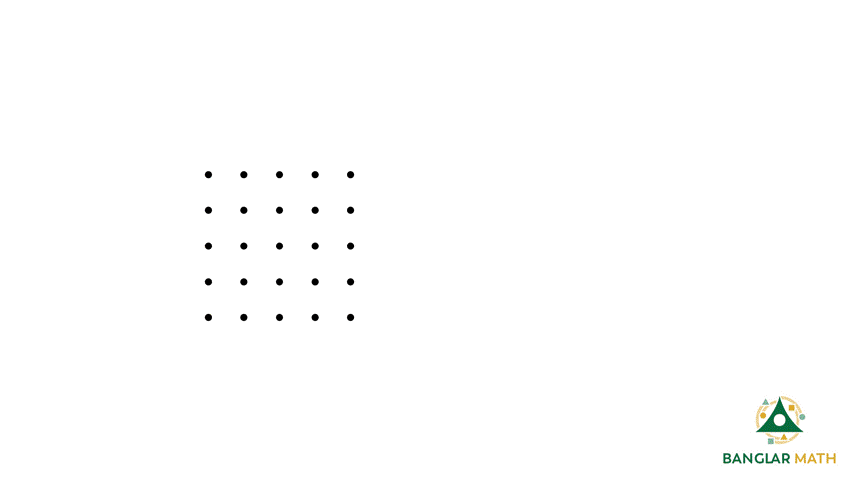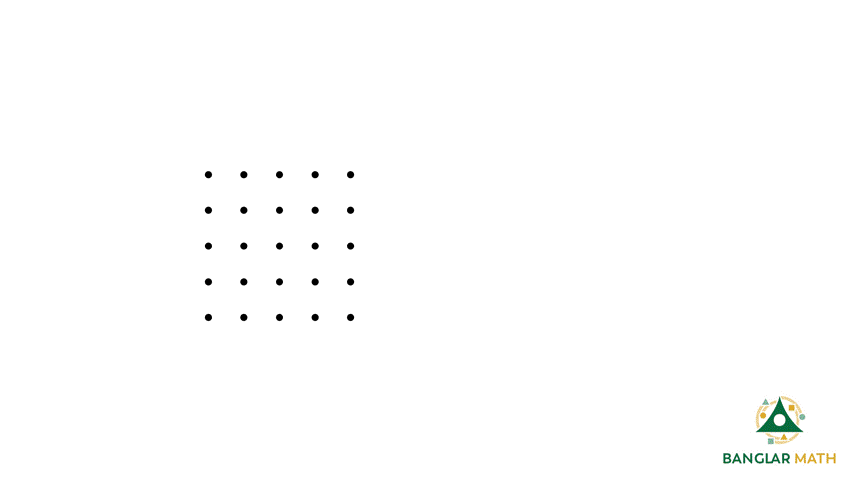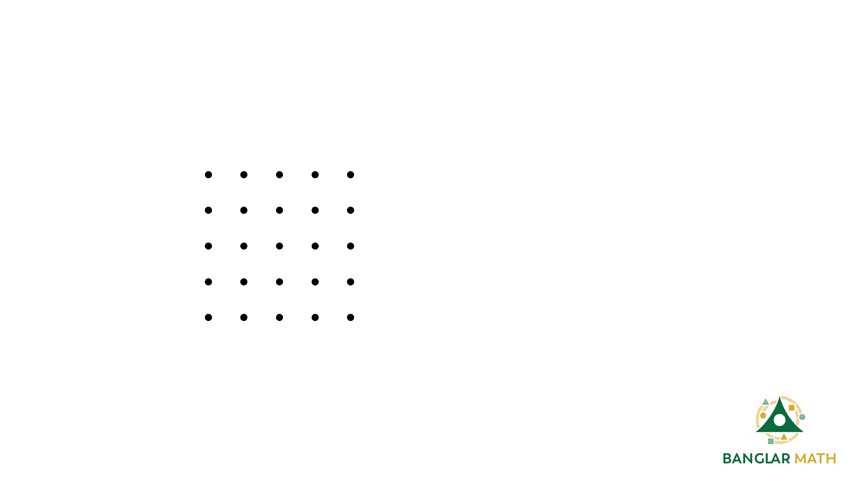Jan 18, 2023 | Problem Weekly (সাপ্তাহিক সমস্যা)
সাপ্তাহিক সমস্যা-১১: জ্যামিতিক জামি তার বোর্ডে কয়েকটি বিন্দু আঁকলো। বিন্দুগুলো গ্রিড পেপারের মত করে সাজানো আছে। জামি এই বিন্দুগুলোর মধ্যে থেকে প্রতিবার চারটি করে বিন্দু নির্বাচিত করে কয়েকটি চতুর্ভুজ অঙ্কন করলো। এই চতুর্ভুজগুলো বিভিন্ন ধরণের, যেমন: কোনটা দেখতে আয়তের মত, আবার কোনটা দেখতে ট্রাপিজিয়ামের মত, কোনটা দেখতে বর্গক্ষেত্রের মতো।
আচ্ছা বলো তো, এই চতুর্ভুজ গুলোর মধ্যে কতটি বর্গক্ষেত্র পাওয়া যাবে?
Problem Weekly-11: Our known guy, Geocentric Jami, drew a few dots on his board. The dots are arranged like grid paper. Jami now selected any four of these points once at a time and, drew some quadrilaterals. These quadrilaterals are of different types, such as a rectangle, trapezium, or a square.
Well, can you tell us how many of them will be squares?
সমাধান: সর্বপ্রথম আমরা খুঁজে দেখি, কোন কোন বাহু বিশিষ্ট বর্গক্ষেত্র এই বিন্দুগুলো যোগ করে তৈরী করা যাবে। একটু খেয়াল করলে দেখবে যে,
কিছু বর্গক্ষেত্র আছে যেখানে বিন্দুগুলো সোজাসুজি যোগ করলেই খুঁজে পাওয়া যাবে, আবার কিছু বর্গক্ষেত্র থাকবে যেগুলো আড়াআড়ি বা বাঁকাভাবে যোগ করলে পাওয়া যাবে। (আড়াআড়ি বোঝার জন্য ঘাড় একটু কাত করে নিতে হবে!)
হিসেবের সুবিধার্থে, আমরা পাশাপাশি দুইটি বিন্দুর দুরত্ব 1 একক ধরে নেই। তাহলে হিসেব করে দেখি, আমরা কয়টা বর্গক্ষেত্র পাবো। এক্ষেত্রে, মোট 16 টি এরকম বর্গক্ষেত্র পাওয়া যাবে। (মিলিয়ে দেখো তো হিসেব ঠিক হয়েছে কি না !)
এবার, আমরা একটি ছক আকারে দেখি মোট কয়টি বর্গক্ষেত্র পাওয়া যাবে-
|
বর্গক্ষেত্রের ধরণ
|
বাহুর দৈর্ঘ্য
|
এরূপ বর্গক্ষেত্রের সংখ্যা
|
|
সোজাসুজি
|
১ একক
|
১৬
|
|
২ একক
|
৯
|
|
৩ একক
|
৪
|
|
৪ একক
|
১
|
|
একটু বাঁকা/
ঘাড় কাত করতে হবে
|
√২ একক*
|
৯
|
|
√৫ একক*
|
৮
|
|
√১০ একক*
|
২
|
|
√৮ একক*
|
১
|
|
মোট
|
৫০
|
(**এই দৈর্ঘ্য গুলো কিভাবে পেলাম সেটির জন্য আমাদেরকে পীথাগোরাসের উপপাদ্য জানতে হবে!)
৫০টি বর্গক্ষেত্রের সমাধান ভালোভাবে বুঝতে নিচের এনিমেশনটি দেখতে পারো-
এটাই আমাদের এ সপ্তাহের গাণিতিক সমস্যার উত্তর। অনেকেই আমাদের কাছে এই সমস্যাটির সমাধান পাঠিয়েছেন, আপনাদের স্বতঃস্ফূর্ত অংশগ্রহণ আমাদের অভিভূত করেছে। মোট ২ জনের সঠিক উত্তর পেয়েছি আমরা, তাই সাপ্তাহিক সমস্যা-১১ এ আমাদের মোট বিজয়ী ২ জন!

যারা উত্তর পাঠিয়েছেন, সবাইকে অভিনন্দন। আশা করি আপনাদের সমস্যা সমাধানের এই যাত্রা অব্যাহত থাকবে।
সবার সেকেন্ড ডিফারেন্সিয়াল নেগেটিভ হোক!
(আমাদের অন্যান্য গাণিতিক সমস্যা দেখতে এই লিঙ্কে ক্লিক করুন।)
Jan 10, 2023 | Problem Weekly (সাপ্তাহিক সমস্যা)
সাপ্তাহিক সমস্যা-১০: আমাদের পরিচিত জ্যামিতিক জামি তার বোর্ডে ইচ্ছেমতো কয়েকটি সংখ্যা লিখলো। সংখ্যাগুলো হলো- 1, 3, 4, 6, 8, 9, 11, 12, 16। এর মাঝে সংখ্যাভাবুক সৌভিক জামির বাসায় এসে হাজির। কিছুক্ষণ পর জামি আর সৌভিক মিলে একটা মজার খেলা শুরু করলো। খেলার নিয়ম খুবই সহজ, প্রত্যেকে বোর্ড থেকে একটা করে সংখ্যা মুছে ফেলবে। প্রথমে সৌভিক একটি সংখ্যা মুছে ফেললো, তখন জামিও একটি সংখ্যা মুছে ফেললো। আবার সৌভিক, আবার জামি, এভাবে খেলা চলতে লাগলো। খেলার এক পর্যায়ে প্রত্যেকে 4টি করে সংখ্যা মুছে ফেললো, তখন দেখা গেলো যে, সৌভিক যে সংখ্যাগুলো মুছে ফেলেছে, সেগুলোর যোগফল জামির মুছে ফেলা সংখ্যার যোগফলের 3 গুন!
সবার শেষে একটি সংখ্যা বোর্ডে রয়ে গেলো। তুমি কি বলতে পারবে সংখ্যাটি কত?
Problem Weekly-10: Our known guy, Geocentric Jami, arbitrarily wrote a few numbers on his board. The numbers are- 1, 3, 4, 6, 8, 9, 11, 12, and 16. In the meantime, the number-lover Souvik appeared at Jami’s house. Then Jami and Souvik started to play an exciting game together. The rule of the game is pretty simple: every person will delete a number from the board! The game started with Souvik; he deleted a number first, then Jami deleted a number. In this way, each deleted 4 numbers at one moment in the game. It turned out that the sum of the numbers that Souvik deleted, was 3 times the sum of the numbers Jami deleted!
One number will remain on the board at the end of the game. Well, can you tell us which number it was?
সমাধান: জামির বোর্ডে লেখা সংখ্যাগুলো হলো- 1, 3, 4, 6, 8, 9, 11, 12, and 16
এই 9 টি সংখ্যার যোগফল হলো- 70
যেহেতু জামি এবং সৌভিক পর্যায়ক্রমে একটি করে সংখ্যা মুছে ফেলেছে, তার মানে তারা প্রত্যেকেই চারটি করে সংখ্যা মুছতে পারবে এবং সবশেষে বোর্ডে একটি সংখ্যা অবশিষ্ট থাকবে।
ধরা যাক, জামির মুছে ফেলা সংখ্যাগুলোর (4 টি সংখ্যা) যোগফল: x
তাহলে, সৌভিকের মুছে ফেলা সংখ্যাগুলোর (4 টি সংখ্যা) যোগফল হবে: 3x
সুতরাং, সবগুলো মুছে ফেলা (8টি সংখ্যা) সংখ্যার যোগফল = 4x
এখান থেকে আমরা বলতে পারি,
জামির মুছে ফেলা সংখ্যার যোগফল + সৌভিকের মুছে ফেলা সংখ্যার যোগফল + অবশিষ্ট সংখ্যা = 70
বা, x + 3x + অবশিষ্ট সংখ্যা = 70
বা, 4x = 70 – অবশিষ্ট সংখ্যা
এই সমীকরণের বাম পাশে রয়েছে 4x যা অবশ্যই 4 দ্বারা বিভাজ্য হবে। তাহলে, ডান পাশে যা থাকবে সেটিও অবশ্যই 4 দ্বারা বিভাজ্য হবে।
এখন, ডানপাশে রয়েছে (70 – অবশিষ্ট সংখ্যা)। এখান থেকে আমরা বলতে পারি, 70 কে 4 দ্বারা ভাগ করলে আমরা যে ভাগশেষ পাবো, বোর্ডের অবশিষ্ট সংখ্যাটিকেও 4 দ্বারা ভাগ করলে একই ভাগশেষ পাবো!
70 কে 4 দ্বারা ভাগ করলে ভাগশেষ থাকবে 2।
অতএব, বোর্ডের অবশিষ্ট সংখ্যাটিকেও 4 দিয়ে ভাগ করলে ভাগশেষ থাকতে হবে 2 (এটা আমরা কিভাবে নিশ্চিত হলাম বলতে পারবে?)
এখন, প্রদত্ত সংখ্যাগুলোর মাঝে একটি সংখ্যাই আছে যাকে 4 দিয়ে ভাগ করলে ভাগশেষ থাকবে 2 এবং সেটি হলো 6।
তার মানে বোর্ডে অবশিষ্ট সংখ্যাটি হলো 6।
সুতরাং, 4x = 70 – 6
বা, 4x = 64
বা, x=16
তাহলে বলা যায়,
জামির মুছে ফেলা সংখ্যা- 1, 3, 4, 8
সৌভিকের মুছে ফেলা সংখ্যা- 9, 11, 12, 16
এবং বোর্ডে থেকে যাওয়া সংখ্যা- 6
এটাই আমাদের এ সপ্তাহের গাণিতিক সমস্যার উত্তর। অনেকেই আমাদের কাছে এই সমস্যাটির সমাধান পাঠিয়েছেন, আপনাদের স্বতঃস্ফূর্ত অংশগ্রহণ আমাদের অভিভূত করেছে। মোট ৫ জনের সঠিক উত্তর পেয়েছি আমরা, তাই সাপ্তাহিক সমস্যা-১০ এ আমাদের মোট বিজয়ী ৫ জন!

যারা উত্তর পাঠিয়েছেন, সবাইকে অভিনন্দন। আশা করি আপনাদের সমস্যা সমাধানের এই যাত্রা অব্যাহত থাকবে। সবার সেকেন্ড ডিফারেন্সিয়াল নেগেটিভ হোক!
(আমাদের অন্যান্য গাণিতিক সমস্যা দেখতে এই লিঙ্কে ক্লিক করুন।)
Jan 4, 2023 | Math Article, Problem Weekly (সাপ্তাহিক সমস্যা)
সাপ্তাহিক সমস্যা-০৯: আমাদের পরিচিত জ্যামিতিক জামি একটি পুরনো গাড়ি কিনেছে। গাড়ি নিয়ে কোথাও গেলে মোট কত দুরত্ব অতিক্রম করা হয়েছে, সেটি দেখা যায়। কিন্তু ঝামেলা হলো, গাড়ির ডিসপ্লে বোর্ডে ৪ অঙ্কটি দেখায় না। এর মানে, গাড়িটিতে যে সংখ্যাগুলো পর্যায়ক্রমে দেখায় তা হলো- ০, ১, ২, ৩, ৫, ৬, ৭, ৮, ৯, ১০, ১১, ১২, ১৩, ১৫……ইত্যাদি। যাই হোক, জামি একদিন সকালে নিজের বাসা থেকে গাড়ি চালিয়ে তার বন্ধু সংখ্যাভাবুক সৌভিকের বাসায় বেড়াতে গেল। সৌভিকের বাড়িতে পৌঁছানোর পর জামি দেখলো যে, গাড়িতে মোট ২০২৩ কি. মি. দুরত্ব দেখাচ্ছে।
জামি তার বাসা থেকে সৌভিকের বাসার আসল দুরত্ব বের করতে চায়। তুমি কি জামিকে সাহায্য করতে পারবে?
Problem Weekly-09: Our known guy, Geometric Jami, has bought an old car. From the display board of the car, it can be seen how far the car has traveled in a trip. But the problem is that the particular digit “4” does not show in the display board of the car. This means that the numbers that appear in the car periodically are- 0, 1, 2, 3, 5, 6, 7, 8, 9, 10, 11, 12, 13, 15…and so on. One morning Jami came out of his house and drove to his friend Number-lover Souvik’s house. Upon reaching Souvik’s house, Jami saw that the car showed a total distance of 2023 km.
Jami wanted to calculate the actual distance from his house to the house of Souvik. Can you help Jami to find the answer?
সমাধান: এ সমস্যা সমাধানের শুরুতেই চলো একটা ছক করে ফেলি। গাড়িতে দেখানো অতিক্রান্ত দুরত্ব বাস্তবে কত দুরত্ব হবে, তার একটা ধারণা পাওয়া যাবে।
|
আসল অতিক্রান্ত দুরত্ব
|
গাড়িতে দেখানো অতিক্রান্ত দুরত্ব
|
|
১
|
১
|
|
২
|
২
|
|
৩
|
৩
|
|
৪
|
৫ (কেননা গাডিতে ৪ সংখ্যাটি দেখায় না)
|
|
৫
|
৬
|
|
৬
|
৭
|
|
৭
|
৮
|
|
৮
|
৯
|
|
৯
|
১০
|
|
১০
|
১১
|
|
১১
|
১২
|
|
১২
|
১৩
|
|
১৩
|
১৫ (কেননা গাডিতে ৪ সংখ্যাটি দেখায় না)
|
|
১৪
|
১৬
|
ছক: গাড়িতে অতিক্রান্ত দুরত্ব বনাম আসল দুরত্ব
এখান থেকে বোঝা যাচ্ছে যে, গাড়িতে দেখানো দুরত্ব আর প্রকৃত অতিক্রান্ত দুরত্ব একই না। তাহলে আমরা বলতে পারি গাড়িতে যত কিলোমিটার দেখাবে আসল দুরত্ব তার চেয়ে কম হবে (তার থেকে কি বেশি হওয়া সম্ভব?)।
আচ্ছা কত কম হবে বলে তোমাদের মনে হয়? ১/ ২/ ৫ না আরো অনেক বেশি? চলো দ্রুত কিছু হিসেব করে ফেলি!
একটু মাথা খাটালে আমরা বুঝবো যে, ১ থেকে শুরু করে গাড়িতে যে সংখ্যা দেখাবে এর মধ্যে যতগুলো ৪ অংক বিশিষ্ট সংখ্যা রয়েছে, ঠিক তত কম হবে আমাদের প্রকৃত অতিক্রান্ত দুরত্ব! কিছুটা কঠিন লাগছে কথাটা? তাহলে কয়েকবার করে পড়ে নিচের সমাধানের সাথে মিলিয়ে নাও।
তাহলে আমরা ঝটপট বের করে ফেলি, ১ থেকে ২০২৩ এর মধ্যে কতগুলো সংখ্যায় ৪ অঙ্কটি আছে।
১ থেকে ৯৯ এর মধ্যে ৪ অঙ্ক রয়েছে মোট- ১৯ টি সংখ্যায় (৪, ১৪, ২৪, ৩৪, ৪০, ৪১, ৪২, ৪৩, ৪৪, ৪৫, ৪৬, ৪৭, ৪৮, ৪৯, ৫৪, ৬৪, ৭৪, ৮৪, ৯৪)।
একইভাবে, ১০০ থেকে ৯৯৯ এর মধ্যে ৪ অঙ্কটি রয়েছে মোট- (১৯ × ৮) +১০০ = ২৫২ বার।
একই ভাবে, ১০০০ থেকে ১৯৯৯ এর মধ্যে ৪ অঙ্কটি রয়েছে মোট- (১৯ × ৯) + ১০০ = ২৭১ বার।
একইভাবে, ২০০০ থেকে ২০২৩ এর মধ্যে ৪ অঙ্কটি রয়েছে মোট- ২ বার।
(আচ্ছা, এই হিসেবগুলো আমরা কি ঠিকঠাক করতে পারলাম? একটু মিলিয়ে নিও তো!)
তাহলে ১ থেকে ২০২৩, এই ব্যবধানে মোট সংখ্যা যেখানে ৪ অঙ্কটি আছে = ১৯ + ২৫২ + ২৭১ + ২ = ৫৪৪ টি
তাহলে জ্যামিতিক জামির বাসা থেকে সংখ্যাভাবুক সৌভিকের বাসার আসল দুরত্ব হলো- (২০২৩-৫৪৪) = ১৪৭৯ কিলোমিটার
এটাই আমাদের এ সপ্তাহের গাণিতিক সমস্যার উত্তর। অনেকেই আমাদের কাছে এই সমস্যাটির সমাধান পাঠিয়েছেন, আপনাদের স্বতঃস্ফূর্ত অংশগ্রহণ আমাদের অভিভূত করেছে। মোট ৪ জনের সঠিক উত্তর পেয়েছি আমরা, তাই সাপ্তাহিক সমস্যা-০৯ এ আমাদের মোট বিজয়ী ৪ জন!

যারা উত্তর পাঠিয়েছেন, সবাইকে অভিনন্দন। আশা করি আপনাদের সমস্যা সমাধানের এই যাত্রা অব্যাহত থাকবে। সবার সেকেন্ড ডিফারেন্সিয়াল নেগেটিভ হোক!
(আমাদের অন্যান্য গাণিতিক সমস্যা দেখতে এই লিঙ্কে ক্লিক করুন।)
Jan 1, 2023 | Math Article, Problem Weekly (সাপ্তাহিক সমস্যা)
পর্ব ৫: সেকেন্ডারি ক্যাটাগরিতে ভালো করার উপায়
সেকেন্ডারি ক্যাটাগরি বলতে মূলত নবম, দশম, এসএসসি পরীক্ষার্থী এবং ও–লেভেলের শিক্ষার্থীদের বুঝায়। এ ক্যাটাগরির ক্ষেত্রে বাছাই পরীক্ষা, আঞ্চলিক পর্যায় এবং জাতীয় পর্বের প্রশ্নগুলোতে একইসাথে একাডেমিক সিলেবাস এবং আন্তর্জাতিক গণিত অলিম্পিয়াড সমমানের প্রস্তুতি, এই দুইটি বিষয়ের উপর বেশি জোর দেয়া হয়। একজন শিক্ষার্থী নবম শ্রেণিতে উঠার পর গণিতের নানা বিষয়ের সাথে প্রথমবারের মতো পরিচিত হয়, যেমন- ত্রিকোণমিতি, জ্যামিতির নতুন কিছু ধারণা, দ্বিপদী, স্থানাংক জ্যামিতি, প্রাথমিক ক্যালকুলাসের ধারণা ইত্যাদি।
একজন শিক্ষার্থীর সেকেন্ডারী ক্যাটাগরির প্রশ্নগুলো আয়ত্ত্বে আনার জন্য গণিতের বিভিন্ন বিষয়ে ভালো ধারণা থাকা দরকার। একইসাথে, শিক্ষার্থীর সমস্যা সমাধানে আগ্রহ থাকা, প্রশ্নগুলো নিয়ে চিন্তা করার অভ্যাস থাকাটাও জরুরী। আজকে আমরা সেকেন্ডারি ক্যাটাগরির বিভিন্ন বিষয় ও কিছু সমস্যা নিয়ে আলোচনা করবো।
বীজগণিত: সেকেন্ডারী ক্যাটাগরির জন্য বিভিন্ন ধরণের ফাংশন, সমীকরণ, অসমতা এই বিষয়গুলো জানা থাকা জরুরী। নিজ শ্রেণির একাডেমিক বই থেকে এই বিষয়গুলো ভালোভাবে আয়ত্ত্ব করতে হবে। পাশাপাশি, এসবের উপর আরো কিছু একাডেমিক বই পড়তে পারলে খুব ভালো হয়। কয়েকটি সমস্যা নিয়ে আমরা আলোচনা করি-

ফাংশনের গাণিতিক সমস্যা নিয়ে কিন্তু অনেকেরই চিন্তা থাকে, কঠিন মনে হয় শিক্ষার্থীদের কাছে। এক্ষেত্রে, একটা উপায় হতে পারে সমস্যাটিকে ছোট ছোট আকারে ভেঙ্গে চিন্তা করা কিংবা ছোট ছোট মানের জন্য ফাংশনের মান বের করা। একটা সমস্যা দেখা যাক-

সংখ্যাতত্ত্ব: সংখ্যা নিয়ে আলোচনা শুরু করা হলে অনেকগুলো বিষয় চলে আসে। যেমন- বিভাজ্যতা, মৌলিক সংখ্যা, ভাগশেষ সংক্রান্ত বিভিন্ন থিওরেম, সংখ্যার উৎপাদক নির্ণয় ইত্যাদি। এ জিনিসগুলো নিয়ে আমরা একাডেমিক বইতে কিছুটা তাত্ত্বিক ধারণা পেলেও চিন্তা করার মত যথেষ্ঠ সমস্যা সাধারণত পাই না । এজন্য, এসব আয়ত্ত্বে আনার উদ্দেশ্যে বিভিন্ন গণিতের বই, আর্টিকেল, ব্লগ ইত্যাদি নিয়মিত পড়া যেতে পারে। আমরা একটি সমস্যা আলোচনা করি-

গণনা: গণনার ক্ষেত্রে মুলত বিন্যাস ও সমাবেশের প্রাথমিক ধারণা থাকা দরকার। নবম-দশম শ্রেণিতে যদিও দ্বিপদী এর একটি অধ্যায় আছে, তবে এর চেয়ে বেশি শিখতে চাইলে একাদশ-দ্বাদশ শ্রেণির বইয়ের বিন্যাস ও সমাবেশ এর অধ্যায় দেখে নিতে হবে। এছাড়া, পিজিওন হোল প্রিন্সিপল, কালারিং, গ্রাফ, সম্ভাব্যতা ইত্যাদি ধারণাগুলোও কাজে লাগে। কিছু কিছু ক্ষেত্রে দেখা যায়, অন্য কোন টপিকের সমস্যার মধ্যে গণনার ধারণা ব্যবহার করে সমাধানে পৌঁছাতে হয়। যেমন নিচের সমস্যাটি দেখা যাক-

জ্যামিতি: জ্যামিতির ক্ষেত্রে সর্বপ্রথম একজন শিক্ষার্থীকে নিজ বইয়ের উপর ভালো দখল রাখতে হবে। আমাদের এনিসিটি বইয়ের জ্যামিতি অংশটুকু চমৎকারভাবে গুছানো আছে। উপপাদ্য নিয়ে পরিষ্কার ধারণা থাকতে হবে। বিশেষ করে, সর্বসমতা কিংবা সদৃশ সংক্রান্ত উপপাদ্য, বৃত্তের ধারণা, এগুলো খুবই কাজে লাগে। উচ্চতর গণিত বইয়ের জ্যামিতি অংশটুকুও বেশ কাজের। এছাড়া, স্থানাংক জ্যামিতি কিংবা ত্রিকোণমিতির ধারণা ব্যবহার করে বিভিন্ন জ্যামিতিক সমস্যার সমাধান খুব সহজে করা যায়। আমরা একটি সমস্যা নিয়ে আলোচনা করি-

আজ এ পর্যন্ত থাক। আশা করছি, এই লিখা থেকে সেকেন্ডারি ক্যাটাগরির প্রস্তুতি নিয়ে একটা ভালো ধারণা পাওয়া গেছে। আসলে অলিম্পিয়াডে ভালো করতে হলে বেশি বেশি সমস্যা সমাধানের কোন বিকল্প নেই। আমাদের সাইটে সাপ্তাহিক সমস্যা বিভাগে বিভিন্ন গাণিতিক সমস্যা দেয়া হয়, কেউ চাইলে এগুলো নিয়মিত সমাধান করতে পারে।
পরবর্তী ব্লগে আমরা হায়ার সেকেন্ডারি ক্যাটাগরির প্রস্তুতি নিয়ে লিখবো। এছাড়াও, বইয়ের তালিকা নিয়ে খুব শীঘ্রই আমাদের আরো ব্লগ প্রকাশিত হবে। সে পর্যন্ত বাংলার ম্যাথের সাথে থাকুন, গণিতের সাথে থাকুন।
Dec 28, 2022 | Math Article, Problem Weekly (সাপ্তাহিক সমস্যা)
সাপ্তাহিক সমস্যা-০৮: সংখ্যা ভাবুক সৌভিক তার বন্ধু জ্যামিতিক জামিকে বিভিন্ন সংখ্যার বর্গ এবং বর্গমূল কিভাবে বের করা যায় সেটি শিখাচ্ছে। কোন একটি সংখ্যাকে ঐ সংখ্যা দিয়েই একবার গুণ করা হলে প্রাপ্ত সংখ্যাকে আমরা বর্গ সংখ্যা বলি।যেমন: 3 × 3 = 9, 5 × 5 = 25 ইত্যাদি। আবার, একই ধারণা দিয়ে কিন্তু বর্গমূলও বের করা যায়। যেমন: √25 = 5, √9 = 3 । কিন্তু খেয়াল রেখো, √26 বা √30 কিন্তু পূর্ণসংখ্যা না! এসব শেখানোর পর সৌভিক জামিকে একটি মজার গাণিতিক সমস্যা দিলো সমাধান করার জন্য। সমস্যাটি ছিলো এরকম:
যদি 1 ≤ a ≤16 এবং 1 ≤ b ≤49 হয়, তাহলে কতগুলো a ও b এর মানের জন্য √(a + √b) এই রাশিটির মান পূর্ণসংখ্যা হবে?
জামি কিছুক্ষণ চেষ্টা করে 10টি সম্ভাব্য উত্তর বের করলো। তোমরা কি বলতে পারবে, জামির উত্তর ঠিক আছে কি না?
Problem Weekly-08: Number-lover Souvik is teaching his friend Geometric Jami how to find the square and square root of different numbers. If a number is multiplied by the same number once, we call it a square number. Like, 3 × 3 = 9, 5 × 5 = 25.
Again, the square root can be derived with the same idea such as √25 = 5, √9 = 3. Note that √26 or √30 are not integers!
After discussing this topic, Souvik gives Jami an interesting problem to find a solution to. The Problem is like that:
If 1 ≤ a ≤16 and 1 ≤ b ≤49, then how many ordered pairs of integer (a, b) are given that the values of √(a + √b) are an integer?
Jami is trying for a while to find out 10 possible answers. Well, can you tell if Jami’s answer is correct or not?
সমাধান: √(a + √b) এর মান তখনই পূর্ণসংখ্যা হবে যখন a + √b এর মান পূর্ণবর্গ সংখ্যা হবে।
যেহেতু a ও b এর অনেকগুলো মান সম্ভব, কাজেই আমাদের দেখতে হবে কোন কোন a ও b এর মানের জন্য a + √b একটি পূর্ণবর্গ সংখ্যা হয়।
প্রশ্নমতে, 1 ≤ b ≤49, তাই √b এর মান হতে পারে শুধুমাত্র 1, 2, 3, 4, 5, 6 এবং 7 (আমরা কিভাবে নিশ্চিত হলাম? ভেবে দেখো তো!)
আচ্ছা, আমরা বর্গসংখ্যার একটা ছক তৈরি করে সম্ভাব্য সমাধান খুঁজে বের করার চেষ্টা করি:
|
a এর মান
|
b এর মান
|
√b এর মান
|
a + √b এর মান
|
√(a + √b) এর মান
|
|
1
|
9
|
3
|
4
|
2
|
|
2
|
4
|
2
|
4
|
2
|
|
2
|
49
|
7
|
9
|
3
|
|
3
|
1
|
1
|
4
|
2
|
|
3
|
36
|
6
|
9
|
3
|
|
4
|
25
|
5
|
9
|
3
|
|
5
|
16
|
4
|
9
|
3
|
|
6
|
9
|
3
|
9
|
3
|
|
7
|
4
|
2
|
9
|
3
|
|
8
|
1
|
1
|
9
|
3
|
|
9
|
49
|
7
|
16
|
4
|
|
10
|
36
|
6
|
16
|
4
|
|
11
|
25
|
5
|
16
|
4
|
|
12
|
16
|
4
|
16
|
4
|
|
13
|
9
|
3
|
16
|
4
|
|
14
|
4
|
2
|
16
|
4
|
|
15
|
1
|
1
|
16
|
4
|
তাহলে সবমিলিয়ে মোট ভিন্ন ভিন্ন 17 টি a এবং b এর মান পাওয়া গিয়েছে যাদের জন্য √(a + √b) এর মান একটি পূর্ণসংখ্যা হবে। অর্থাৎ, জামির উত্তর ভুল ছিলো!
অনেকেই আমাদের কাছে এই সমস্যাটির সমাধান পাঠিয়েছেন, আপনাদের স্বতঃস্ফূর্ত অংশগ্রহণ আমাদের অভিভূত করেছে। মোট ৯ জনের সঠিক উত্তর পেয়েছি। তাই সাপ্তাহিক সমস্যা-০৮ এ আমাদের মোট বিজয়ী ৯ জন।
যারা উত্তর পাঠিয়েছেন, সবাইকে অভিনন্দন। আশা করি আপনাদের সমস্যা সমাধানের এই যাত্রা অব্যাহত থাকবে।
সবার সেকেন্ড ডিফারেন্সিয়াল নেগেটিভ হোক!
(আমাদের অন্যান্য গাণিতিক সমস্যা দেখতে এই লিঙ্কে ক্লিক করুন।)
Dec 20, 2022 | Math Article, Problem Weekly (সাপ্তাহিক সমস্যা)
সাপ্তাহিক সমস্যা-০৭: জ্যামিতিক জামি তার রুমের দেয়ালে একটি মাল্টিকালারের বোর্ড বসিয়েছে। জামির ইচ্ছা তার বোর্ডে সারাদিন ধরে বিভিন্ন জ্যামিতিক ছবি আকঁবে। বোর্ডটিতে তিনটি রঙ আছে। সংখ্যাভাবুক সৌভিক জামিদের বাসায় একদিন বেড়াতে এসে এরকম বোর্ড দেখে অনেক খুশী হলো। সৌভিক বোর্ডের পরিমাপ জিজ্ঞেস করলে জামি উত্তর দিলো যে, সে পুরোপুরি মাপ জানে না। তবে সে কিছু তথ্য দিলো সৌভিককে। সৌভিক কিছুক্ষণ চিন্তা করে বোর্ডটির দৈর্ঘ্য প্রস্থ সবকিছু একসাথে বলে দিলো। আচ্ছা, তোমরা কি সৌভিকের মত চিত্রের দেয়া তথ্য থেকে বোর্ডটির পরিসীমা বের করতে পারবে?
Problem Weekly-07: Geo-centric Jamie has placed a multicolor board on the wall of his room. Jamie wishes to draw various geometric pictures on his board throughout the day. There are three colors on the board. One day, Souvik came to visit Jami’s house and became very happy to see such a board. When Souvik asked for the dimension of the board, Jami replied that he did not know all the dimension. However, Jami gave some information to Souvik regarding the board. Souvik thought for a while and said everything about the length and breadth of the board. Well, from the given diagram, can you figure out the perimeter of the board like Souvik?
সমাধান: চিত্র অনুযায়ী লাল, হলুদ এবং সবুজ রঙ দ্বারা চিহ্নিত অংশের উচ্চতা বা দৈর্ঘ্য একই।
ধরি, বোর্ডের উচ্চতা = y একক
তাহলে লাল এবং হলুদ রঙ দ্বারা চিহ্নিত অংশের ক্ষেত্রফল হবে-
10y = 120 + x … … …(i)
আর সবুজ এবং হলুদ রঙ দ্বারা চিহ্নিত অংশের ক্ষেত্রফল হবে-
12y = 150 + x … … …(ii)
এখন (ii)নং সমীকরণ থেকে (i)নং সমীকরণ বিয়োগ করে পাই-
12y – 10y = 150 + x – (120 + x)
বা, 2y = 30
বা, y = 15
তাহলে, সবুজ রঙ চিহ্নিত অংশের প্রস্থ আমরা সহজেই বের করতে পারবো।
যেহেতু, ক্ষেত্রফল = উচ্চতা × প্রস্থ। সুতরাং,
150 = 15 × প্রস্থ
বা, প্রস্থ = 10 একক
তাহলে, হলুদ রঙ চিহ্নিত অংশের প্রস্থ = 12 – 10 = 2 একক
সুতরাং, বোর্ডের পরিসীমা আমরা পাবো-
15 + (10 – 2) + 2 + (12 – 2) + 15 + (10 – 2) + 2 + (12 – 2) = 70 একক
এটাই আমাদের এ সপ্তাহের গাণিতিক সমস্যার উত্তর!
অনেকেই আমাদের কাছে এই সমস্যাটির সমাধান পাঠিয়েছেন। মোট ৯ জনের সঠিক উত্তর পেয়েছি।
তাই সাপ্তাহিক সমস্যা-০৭ এ আমাদের মোট বিজয়ী ৯ জন।
যারা উত্তর পাঠিয়েছেন, সবাইকে অভিনন্দন। আশা করি আপনাদের সমস্যা সমাধানের এই যাত্রা অব্যাহত থাকবে।
সবার সেকেন্ড ডিফারেন্সিয়াল নেগেটিভ হোক!
(আমাদের অন্যান্য গাণিতিক সমস্যা দেখতে এই লিঙ্কে ক্লিক করুন।)