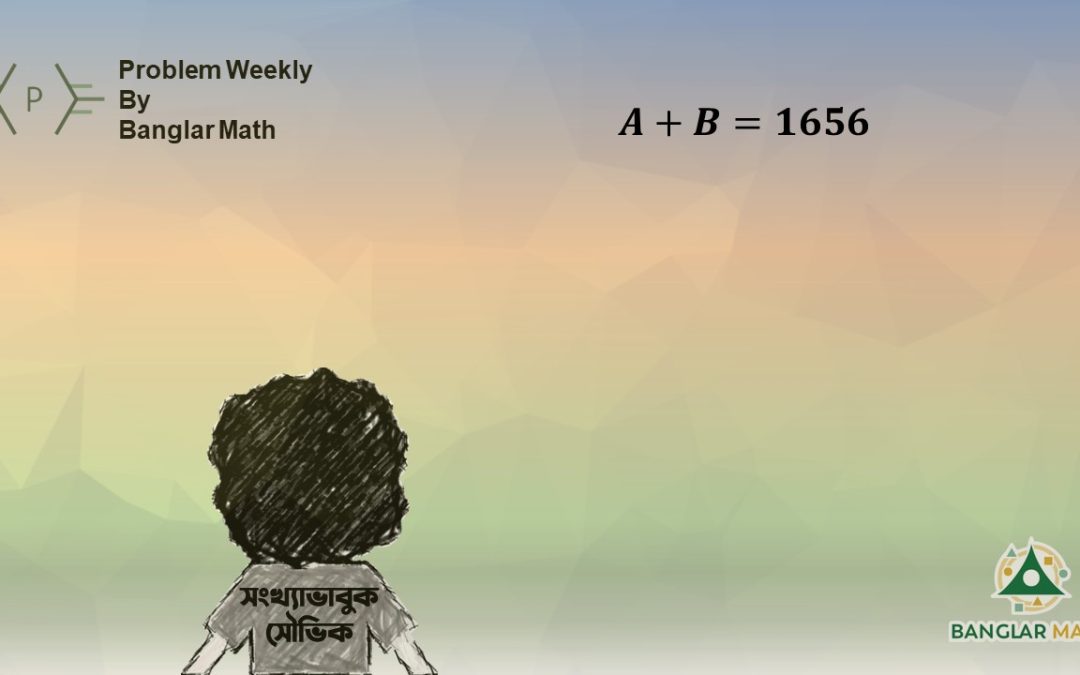সাপ্তাহিক সমস্যা-২৮: সংখ্যাভাবুক সৌভিক বরাবরের মত আজকেও সংখ্যা নিয়ে ভাবছে। সে নিজের খাতায় একটি তিন-অংকের সংখ্যা “A” লিখলো। আবার সে খেয়াল করলো যে, সংখ্যাটির অংকগুলো উল্টিয়ে লিখলে আরেকটি নতুন তিন অংকের সংখ্যা “B” পাওয়া যায়। সৌভিক হিসেব করে দেখলো, এ দুইটি তিন অংকের সংখ্যা যোগ করলে যোগফল 1656 হয়।
আচ্ছা, সৌভিক প্রথমে কোন সংখ্যাটি লিখেছিলো সেটা কী তুমি বলতে পারবে?
Problem Weekly-28: Number-lover Souvik is thinking about numbers as always. He has written a random three-digit number “A” in his notebook. Again, he has noticed that if the digits of the number “A” are reversed, a three-digit number “B” is obtained. Then Sauvik adds these two three-digit numbers and has got the sum to be 1656.
Can you tell us which number Souvik wrote at first?
সমাধান: যেহেতু A একটি তিন অংকের সংখ্যা তাই আমরা লিখতে পারি-
A = 100a + 10b + c
[এখানে a, c এর মান 0 হবে না, এদের মান 9 এর সমান বা তার থেকে ছোট হবে, এবং 0 <= b <= 9 হবে]
যেমন 714 কে আমরা এভাবে লিখতে পারি-
714 = 7 × 100 + 1 × 10 + 4
যেহেতু A সংখ্যাটির অঙ্কগুলো উল্টিয়ে লিখলে একটি তিন অঙ্কের সংখ্যা B পাওয়া যায়, তাই আমরা লিখতে পারি-
B = 100c + 10b + a
প্রশ্নমতে,
A + B = 1656
বা, 100a + 10b + c + 100c + 10b + a = 1656
বা, 101a + 20b + 101c = 1656
বা, 20b = 1656 – 101(a+c)
বা, b = [1656 – 101 (a+c)] / 20
যেহেতু b একটি পূর্ণসংখ্যা, তার মানে ডানপাশের ভগ্নাংশের লবকে অবশ্যই 20 দ্বারা বিভাজ্য হতে হবে বা লবের সংখ্যাটির একক স্থানীয় অঙ্ক 1 হতে হবে। (এটা কেন নিশ্চিত করে বলতে পারলাম? চিন্তা করে দেখো তো!)
তাহলে, (a+c) এর মান 6 বা 16 হতে হবে।
কিন্তু (a+c) এর মান 6 হলে b এর মান 9 এর চেয়ে বড় হয়ে যায় যেটা প্রদত্ত তথ্য অনুসারে সম্ভব না। (কারণ b এর মান 5 হতে পারবে।)
তাহলে বলা যায়,
(a+c) = 16
এবং b এর মান হবে-
b = [1656 – (101 × 16)] / 20
যেহেতু (a+c) = 16, তাহলে a এবং c এর সম্ভাব্য মান হবে-
(a, c) = (9, 7) , (8, 8), (7, 9)
তাহলে সৌভিক শুরুতে যে সংখ্যাটি লিখেছিল তার সম্ভাব্য মান হতে পারে, 927 বা 828 বা 729।
সুতরাং, উপরের তিনটি সংখ্যাই হচ্ছে আমাদের সাপ্তাহিক সমস্যা-২৮ এর উত্তর!
অনেকেই আমাদের কাছে এই গাণিতিক সমস্যাটির সমাধান পাঠিয়েছে, সবার স্বতঃস্ফূর্ত অংশগ্রহণ আমাদের অভিভূত করেছে। তবে আমরা ৩ জনের সঠিক উত্তর পেয়েছি, তাই সাপ্তাহিক সমস্যা-২৮ এ বিজয়ী তিনজন!

ছবি: সাপ্তাহিক সমস্যা-২৮ এর বিজয়ী তালিকা
যারা সমস্যাটির সমাধান করার চেষ্টা করেছো, সবাইকে অভিনন্দন। আশা করি তোমাদের সমস্যা সমাধানের এই চেষ্টা অব্যাহত থাকবে। তোমাদের সবার সেকেন্ড ডিফারেন্সিয়াল নেগেটিভ হোক!
(আমাদের অন্যান্য গাণিতিক সমস্যা দেখতে এই লিঙ্কে ক্লিক করুন।)