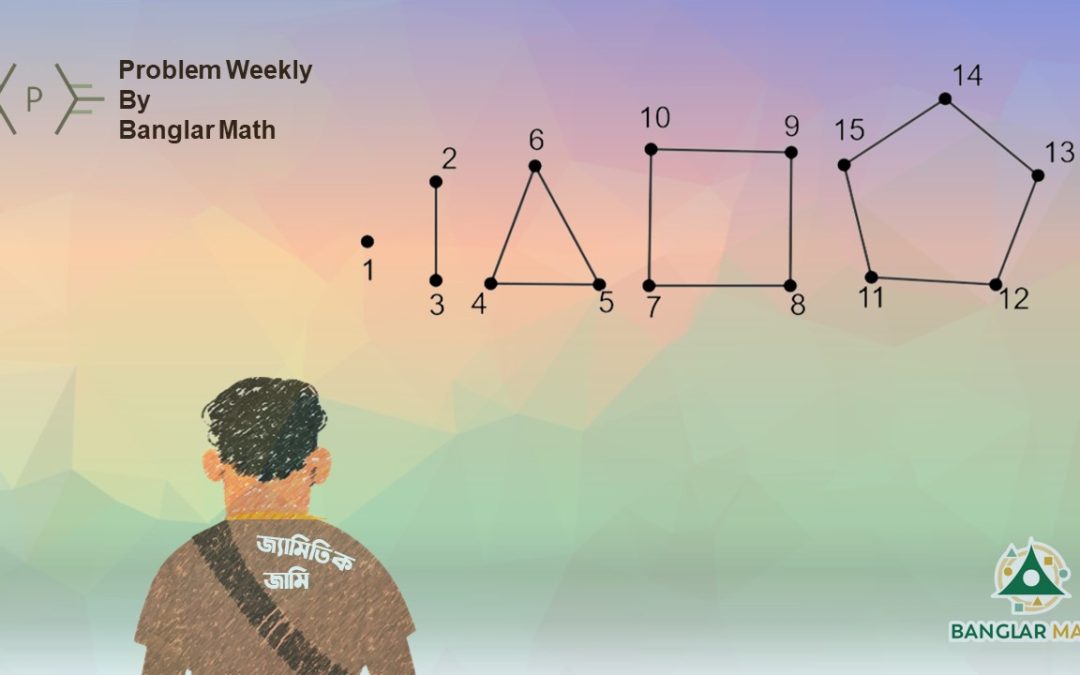
সাপ্তাহিক সমস্যা-২৩: জ্যামিতিক জামি নিজের ইচ্ছেমতো খাতায় বিভিন্ন জ্যামিতিক ছবি আঁকছে। প্রথমে সে একটা বিন্দু আঁকলো, এরপর রেখাংশ, এর পর ত্রিভুজ, চতুর্ভুজ, পঞ্চভূজ, এভাবে করে সে বিভিন্ন বহুভূজ আঁকতে লাগলো। এর পাশাপাশি সে জ্যামিতিক চিত্রগুলোর শীর্ষবিন্দুকে ১, ২, ৩, ৪….. এভাবে ক্রমানুসারে নম্বর দিয়ে চিহ্নিত করতে লাগলো।
এখন প্রশ্ন হলো, জামি যে জ্যামিতিক ছবির শীর্ষবিন্দুতে ২০২৩ সংখ্যাটি লিখবে, সেখানে কয়টি বাহু থাকবে? সমাধান নিয়ে চিন্তা করা শুরু করো তাহলে!
Problem Weekly-23: Geometric Jami is drawing various geometric figures as he likes in his notebook. First, he drew a point, then a line segment, then a triangle, quadrilateral, pentagon, and so on, he started drawing different polygons. Besides this, he began to mark the vertices of geometric figures with serial numbers
1, 2, 3, 4……
Now, how many sides will there be in the geometric figure that Jami will write the number 2023? Let’s start thinking about the solution!
সমাধান: আমরা যদি শীর্ষবিন্দুগুলো গণনা শুরু করি, তাহলে দেখতে পাবো যে শীর্ষবিন্দুগুলোর সংখ্যাগুলো হবে-
1+2+3+4+5+6………
আমরা নিচের ছকে একটু হিসেব করে দেখি কোন জ্যামিতিক চিত্রে বিন্দুর সংখ্যা কয়টি হবে-
|
জ্যামিতিক চিত্রের নাম |
বিন্দুর সংখ্যা |
মোট বিন্দুর সংখ্যা |
|
বিন্দু (Point) |
1 |
1 |
|
রেখাংশ (Line Segment) |
2 |
3 |
|
ত্রিভুজ (Triangle) |
3 |
6 |
|
চতুর্ভুজ (Quadrilateral) |
4 |
10 |
|
৫ বাহু বিশিষ্ট বহুভূজ (Pentagon) |
5 |
15 |
|
৬ বাহু বিশিষ্ট বহুভূজ (Hexagon) |
6 |
21 |
|
৭ বাহু বিশিষ্ট বহুভূজ (Heptagon) |
7 |
28 |
একটু চিন্তা করলে বুঝতে পারবে, এখানে মোট বিন্দুর সংখ্যা মূলত 1 থেকে শুরু করে প্রথম n সংখ্যক ধনাত্মক সংখ্যার যোগফল। আমরা গাউসের সূত্র বা সমান্তর ধারার সূত্র থেকে জানি যে-
প্রথম n সংখ্যক ধনাত্মক সংখ্যার যোগফল হবে- [n(n+1)/2]
নিচের ছকে তাহলে একটু হিসেব করে দেখি n এর বিভিন্ন মানের জন্য বিন্দুর সংখ্যা কেমন হবে-
|
n এর মান |
মোট বিন্দুর সংখ্যা |
|
40 |
820 |
|
50 |
1275 |
|
60 |
1830 |
|
70 |
2485 |
|
65 |
2145 |
|
63 |
2016 |
|
64 |
2080 |
খেয়াল করে দেখো, n এর মান 63 হলে মোট বিন্দুর সংখ্যা আমরা পাচ্ছি 2016, n এর মান 64 হলে আমরা পাচ্ছি 2080।
সুতরাং, 64 বাহু বিশিষ্ট বহুভূজের শীর্ষবিন্দুতে 2023 লিখা থাকবে। এটাই আমাদের এই সপ্তাহের গাণিতিক সমস্যার উত্তর!
আমরা এই সমস্যাটির একটি বিকল্প সমাধানও চিন্তা করতে পারি। অসমতা ব্যবহার করলে সমস্যটির সমাধান এরকম হবে-
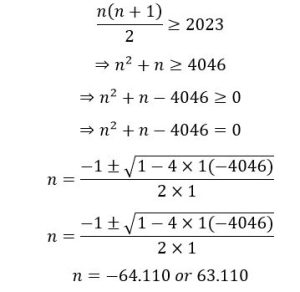
n এর সর্বনিম্ন মান তাহলে 64 হবে। অর্থাৎ, 64 বাহু বিশিষ্ট বহুভূজের শীর্ষবিন্দুতে 2023 লিখা থাকবে।
অনেকেই আমাদের কাছে এই গাণিতিক সমস্যাটির সমাধান পাঠিয়েছে, সবার স্বতঃস্ফূর্ত অংশগ্রহণ আমাদের অভিভূত করেছে। তবে আমরা ২ জনের সঠিক উত্তর পেয়েছি, তাই সাপ্তাহিক সমস্যা-২৩ এ বিজয়ী দুইজন!

ছবি: সাপ্তাহিক সমস্যা-২৩ এর বিজয়ী তালিকা
যারা সমস্যাটির সমাধান করার চেষ্টা করেছো, সবাইকে অভিনন্দন। আশা করি তোমাদের সমস্যা সমাধানের এই চেষ্টা অব্যাহত থাকবে। তোমাদের সবার সেকেন্ড ডিফারেন্সিয়াল নেগেটিভ হোক!
(আমাদের অন্যান্য গাণিতিক সমস্যা দেখতে এই লিঙ্কে ক্লিক করুন।)