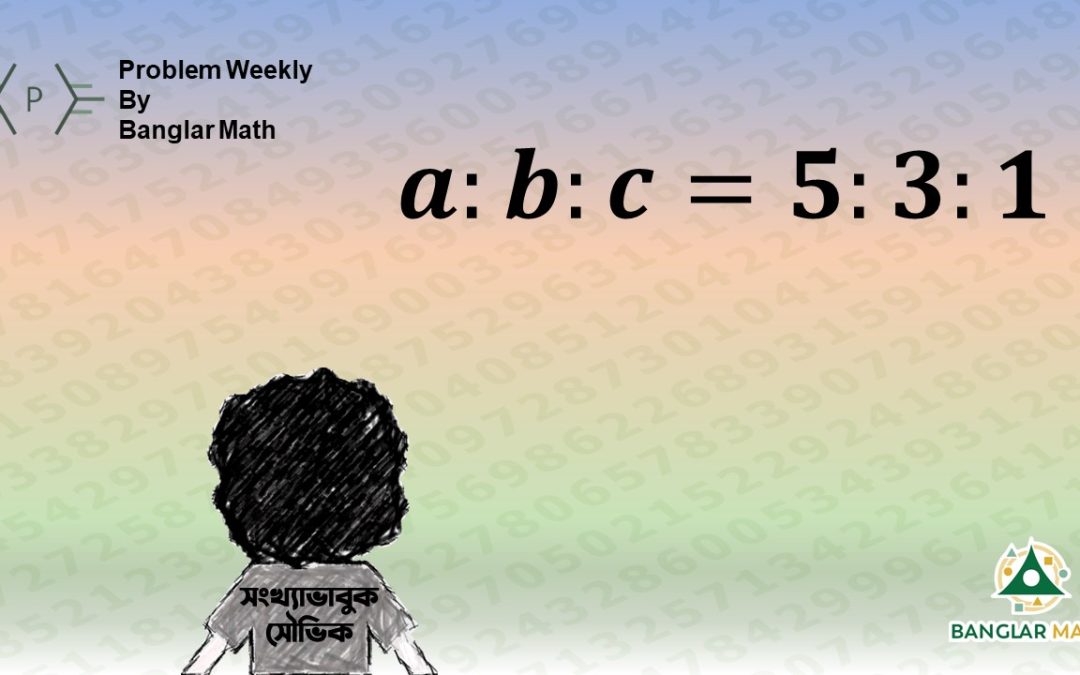সাপ্তাহিক সমস্যা-১৯: সংখ্যাভাবুক সৌভিক প্রতিদিনের মত আজকে সকালে নিজের খাতায় 1 থেকে 9 পর্যন্ত অঙ্কগুলো ব্যবহার করে বিভিন্ন সংখ্যা তৈরী করছে। হঠাৎ করে সৌভিক একটা মজার বিষয় লক্ষ করলো; সে নিজের খাতায় তিনটি সংখ্যা লিখেছে এবং এই তিনটি সংখ্যার মধ্যে সবথেকে বড় সংখ্যাটি হল সবচেয়ে ছোট সংখ্যার পাঁচগুণ! আর অপর যে সংখ্যাটি রয়েছে, সেটি সবচেয়ে ছোট সংখ্যাটির তিনগুণ!
সহজে বোঝার সুবিধার্থে বলা যায়, যদি তিনটি সংখ্যা যথাক্রমে a, b, c হয় যেখানে a> b> c, তাহলে, a:b:c = 5:3:1 লিখা যায়। শুধুমাত্র ১ থেকে ৯ – এই নয়টি অঙ্ক একবার করে ব্যবহার করে সৌভিক সংখ্যা তিনটি লিখেছে।
আচ্ছা, তোমরা কি সৌভিকের এই তিনটি সংখ্যা বের করতে পারবে?
Problem Weekly-19: Number-lover Souvik makes different numbers by using the digits from 1 to 9 in his notebook like every day. Suddenly Sauvik noticed something interesting; he wrote three numbers in his notebook. Interestingly, among these three numbers, the largest is five times the smallest. And the other number is three times the smallest number!
To explain the statement clearly, let’s say if three numbers are a, b, and c respectively where a> b> c, then we can say a:b:c = 5:3:1. Using the nine digits from 1 to 9 only once, Sauvik writes these three numbers.
Well, can you figure out these three numbers?
সমাধান: যেহেতু, a:b:c = 5:3:1 বা a সংখ্যাটি হবে c সংখ্যার পাঁচগুণ, b সংখ্যাটি হবে c সংখ্যার তিনগুণ, এবং ১ থেকে ৯ অঙ্কগুলো একবার করে ব্যবহৃত হয়েছে,
তাহলে আমরা বলতে পারি যে, c সংখ্যাটি এক অঙ্ক বা দুই অঙ্কের হতে পারবে না, অন্তত তিন অঙ্কের হতে হবে। কারণ c যদি এক অঙ্ক বা দুই অঙ্কের হয়, সেক্ষেত্রে b কিংবা a সর্বোচ্চ তিন অঙ্কের হবে, তখন ৮টি অঙ্কের বেশি ব্যবহার করার সুযোগ থাকবে না। এছাড়া c সংখ্যাটি তিন অঙ্কের বেশিও হতে পারবে না, সেক্ষেত্রে আমাদের শর্ত ভঙ্গ হবে!
তাহলে আমরা নিশ্চিত যে, c সংখ্যাটি তিন অঙ্কের হবে। এখন c এর শতক স্থানীয় অঙ্কে 1 অঙ্কটি বসাতে হবে, শতক স্থানীয় অঙ্কে 1 বাদে কোন অঙ্ক বসলে বৃহত্তম সংখ্যা a চার অঙ্ক বিশিষ্ট সংখ্যায় পরিণত হবে যা শর্ত ভঙ্গ করে! আবার, c এর একক স্থানীয় অঙ্কে কোন জোড় অঙ্ক বসতে পারবে না, কেননা জোড় সংখ্যা বসলে a সংখ্যাটির একক স্থানীয় অঙ্কটিকে ০ হতে হবে যা প্রদত্ত শর্তের বাইরে।
একইভাবে, c এর একক স্থানীয় অঙ্কে 5 বসতে পারবে না, কেননা a এর একক স্থানীয় অঙ্ক সেক্ষেত্রে 5 হবে যা সম্ভব না। (কেন বলো তো!)
একই নিয়মে, c এর একক স্থানীয় অঙ্কে 7 বসতে পারবে না, কেননা b এর একক স্থানীয় অঙ্ক 1 হতে পারবে না!
তাহলে বলা যায়, c এর একক স্থানীয় অঙ্কে হয় 3 অথবা 9 অঙ্কটি বসবে।
যদি c এর একক স্থানীয় অঙ্ক 3 হয়, তাহলে b এর একক স্থানীয় অঙ্ক 9 হবে এবং a এর একক স্থানীয় অঙ্ক হবে 5।
আবার, b এর শতক স্থানীয় অঙ্ককে অবশ্যই 3, 4 কিংবা 5 হতে হবে কেননা c এর শতক স্থানীয় অঙ্ক 1।
আগের শর্ত থেকে, যদি c এর একক স্থানীয় অঙ্ক 3 হয়, তাহলে b এর শতক স্থানীয় অঙ্ককে 4 হতে হবে। (ভেবে দেখো কেন এটা হবে!)
সেক্ষেত্রে আমরা যে অঙ্কগুলো ব্যবহার করেছি সেগুলো হলো 1, 3, 4, 5, 9। বাকি অংকগুলো হলো- 2, 6, 7, 8।
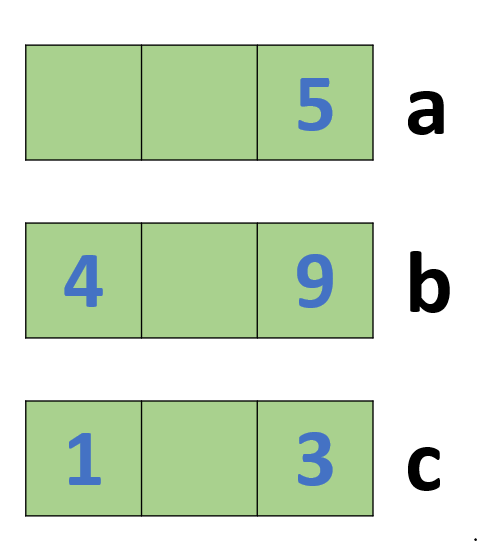
ছবি: c সংখ্যার জন্য় এককের ঘরে 3 অঙ্কটি বসেছে
এখন c এর দশক স্থানীয় অঙ্ক হিসেবে যে অঙ্কগুলো বসতে পারে সেগুলো হলো- 2, 6, 7, 8। কিন্তু এদের কোনোটাই বসতে পারবে না! কারণ c এর দশক স্থানীয় অঙ্ক 2 বা 6 বা 7 বা 8 হলে b এর শতক স্থানীয় অঙ্ক হিসেবে 4 কোনোভাবেই বসতে পারবে না এবং প্রতিবারই এই অঙ্কগুলোর জন্য বাকি সংখ্যাতে একই অঙ্ক একাধিকবার চলে আসে কিংবা ১-৯ পর্যন্ত সবগুলো অঙ্ক একবার করে ব্যবহারের সুযোগ থাকে না। অর্থাৎ, c এর একক স্থানীয় অঙ্কে 3 বসানো যাবে না।
তাহলে, c এর একক স্থানীয় জায়গায় ৯ অঙ্কটিই বসবে! সেক্ষেত্রে, b এর একক স্থানীয় অঙ্কে 7 বসবে এবং a সংখ্যাটির একক স্থানীয় অঙ্কে 5 বসবে।
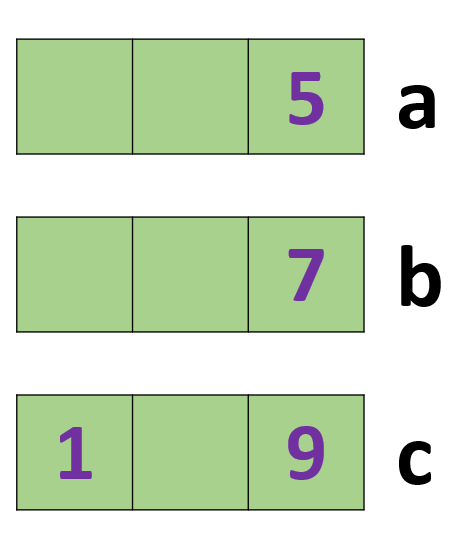
ছবি: c সংখ্যার জন্য় এককের ঘরে 9 অঙ্কটি বসেছে
কিন্তু আমরা শুধুমাত্র c এর দশক স্থানীয় অঙ্কে 2 বসিয়ে সমাধান পাবো, বাকি অঙ্কগুলোর জন্য সমাধান আসবে না, কোন না কোন শর্ত অমান্য হবেই।
(তুমি চাইলে হিসেব করে দেখতে পারো আমাদের উত্তর ঠিক না ভুল হয়েছে!)
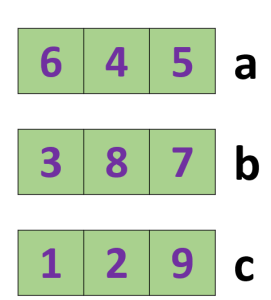
ছবি: c, b এবং a সংখ্যা তিনটির সঠিক মান
সুতরাং, c এর মান হবে 129, b এর মান হবে 387, এবং a এর মান হবে 645 । এটাই আমাদের এই এই সপ্তাহের গাণিতিক সমস্যার উত্তর!
অনেকেই আমাদের কাছে এই গাণিতিক সমস্যাটির সমাধান পাঠিয়েছে, সবার স্বতঃস্ফূর্ত অংশগ্রহণ আমাদের অভিভূত করেছে। শুধুমাত্র ১ জনের সঠিক উত্তর পেয়েছি, তাই সাপ্তাহিক সমস্যা-১৯ এ আমাদের বিজয়ী ১ জন!

ছবি: সাপ্তাহিক সমস্যা-১৯ এর বিজয়ী তালিকা
যারা উত্তর পাঠিয়েছেন, সবাইকে অভিনন্দন। আশা করি আপনাদের সমস্যা সমাধানের এই যাত্রা অব্যাহত থাকবে। সবার সেকেন্ড ডিফারেন্সিয়াল নেগেটিভ হোক!
(আমাদের অন্যান্য গাণিতিক সমস্যা দেখতে এই লিঙ্কে ক্লিক করুন।)