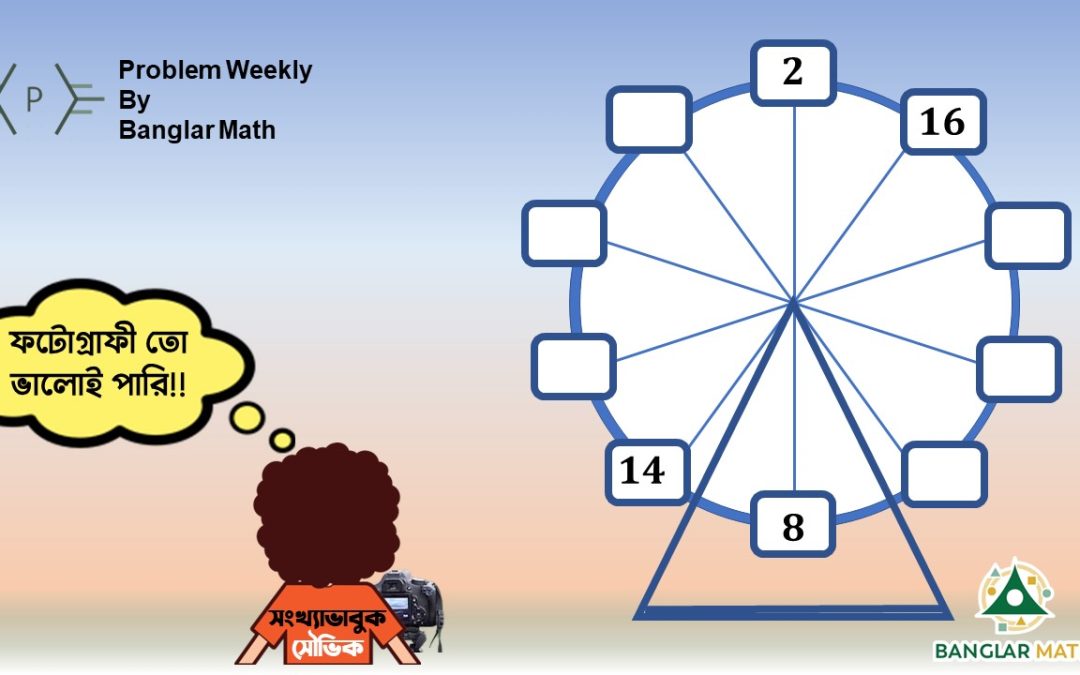
সাপ্তাহিক সমস্যা-০৬: সংখ্যাভাবুক সৌভিক তার স্কুলের ফুটবল টিমে খেলার সুযোগ পেয়েছে। সামনেই একটা টুর্নামেন্ট আছে। টুর্নামেন্টের আগে আগে চাপ মুক্ত থাকার জন্য সৌভিক তার দলের সবাইকে নিয়ে মেলায় ঘুরতে গেলো। মেলাতে বিভিন্ন ধরণের বিনোদনের ব্যবস্থা ছিল; ছিল নাগরদোলায় চড়ার ব্যবস্থা, ছিল সার্কাস, পুতুল নাচ ইত্যাদি।দলের সবাই মিলে ঠিক করলো নাগরদোলায় উঠবে। সবাই নাগরদোলায় চড়ে বসলো আর সৌভিক ছবি তোলার জন্য নিচে থেকে গেলো। কিছু ছবি তোলার পর সৌভিক দেখতে লাগলো ছবিগুলো কেমন হয়ছে। দেখার পর মনে মনে বললো , ছবি তো সুন্দরভাবেই উঠেছে! কিচ্ছুক্ষণ পর সৌভিক খেয়াল করলো যে, নাগরদোলায় ১০ জন যেভাবে বসেছে ,তাদের মধ্যে সুন্দর একটা গাণিতিক মিল আছে। পাশাপাশি বসা দুইজন খেলোয়াড়ের জার্সির নম্বরের বর্গের যোগফল, তাদের ঠিক বিপরীতে যে দুইজন খেলোয়াড় বসেছে, তাদের জার্সির নম্বরের বর্গের যোগফলের সমান!
এখানে, ছবিতে চার জনের জার্সি নম্বর দেয়া আছে। তোমরা কি বলতে পারবে যে ,বাকি ছয় জন খেলোয়াড়ের জার্সি নম্বরের যোগফল কত হবে?
Problem Weekly-06: Number-lover Souvik has got a chance on his school team to play football. There’s a tournament ahead. Before the tournament, Souvik and his team went to the fair together to stay stress-free. There were various types of entertainment at the fair; there were arrangements for climbing in Nagardola, there were circuses, puppet-show, etc. The team decided to ride on the mighty “Nagordola”. Leaving Souvik, the rest of the team sat on Nagardola and gave Souvik the responsibility of taking pictures of them. So after taking the pictures, Souvik checked the quality of the pictures and said to himself, “The pictures are beautifully taken.” After some moment, Souvik somehow noticed that there was a beautiful mathematical similarity between the 10 players sitting in Nagardola. That is, the sum of the squares of the jersey number of two players is equal to the sum of the squares of the jersey number of two players who sit opposite them.
In the picture below, the jersey number of four players is given. Can you say what will be the sum of the jersey number of the remaining six?
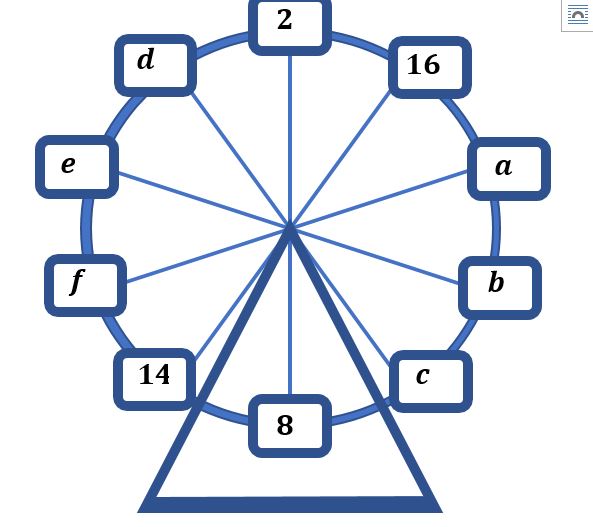
সমাধান: ধরি, বাকি ছয় জনের জার্সির নম্বর যথাক্রমে a, b, c, d, e, এবং f
তাহলে, প্রশ্নের তথ্যানুসারে,
a2 + b2 = f2 + e2 ……..(i)
b2 + c2 = e2+ d2 ……..(ii)
c2+ 82 = d2 + 22 ……..(iii)
142 + f2 = 162 + a2 ………(iv)
(i) নং সমীকরণ হতে পাই,
b2 – e2 = f2 – a2
(ii) নং সমীকরণ হতে পাই,
b2 – e2 = d2 – c2
(iii) নং সমীকরণ হতে পাই,
d2 – c2 = 82 – 22
বা, d2 – c2 = 60
এখান থেকে সমীকরণ সমন্বয় করে আমরা বলতে পারি যে,
b2 – e2 = f2 – a2 = d2 – c2 = 60
বা, (b + e) (b – e) = (f + a) (f – a) =
(d + c) (d – c) = 60
এখন, আমাদের 60 এর উৎপাদকগুলো খুঁজে বের করতে হবে। 60 এর উৎপাদকগুলো হল:
60 = 1 × 60
= 2 × 30
= 3 × 20
= 4 × 15
= 5× 12
= 6 × 10
এখন, 60 কে আমাদের দুইটি রাশির গুণফল আকারে প্রকাশ করতে হবে। যেমন:
(b + e) (b – e) = 60।
এক্ষেত্রে, দুইটি রাশির প্রত্যেকটি সংখ্যা অবশ্যই জোড় অথবা বিজোড় হতে হবে। কোন একটি রাশির একটি সংখ্যা জোড় এবং অপরটি বিজোড় হতে পারবে না যেহেতু গুণফল একটি জোড় সংখ্যা!
কাজেই, আমরা বলতে পারি,
(b + e) (b – e) = 6 × 10 এবং
(b + e) (b – e) = 2 × 30
এই দুটোই সম্ভাব্য সমাধান হতে পারে।
সুতরাং, আমাদের সমাধান অনুসারে
(b, e) = (8,2) অথবা (16, 14) হবে।
একইভাবে,
(f, a) = (8,2) বা (16, 14)
(d, c) = (8,2) বা (16, 14)
তাহলে, বাকি ছয়জনের জার্সি নম্বরের যোগফল হতে পারে 30 কিংবা 50 কিংবা 70 কিংবা 90।
কিভাবে আমরা এটা বলতে পারলাম?
নিচে দুইটি উদাহরণ দেখানো হল:
যখন a = 2, b = 8, c = 2, d = 8, e = 2, f = 8 হবে, তখন যোগফল হবে 30।
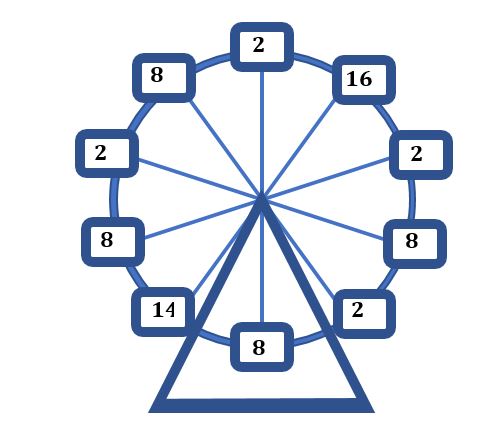
আবার, যখন a = 2, b = 16, c = 2, d = 8, e = 14, f = 8 হবে, তখন যোগফল হবে 50।
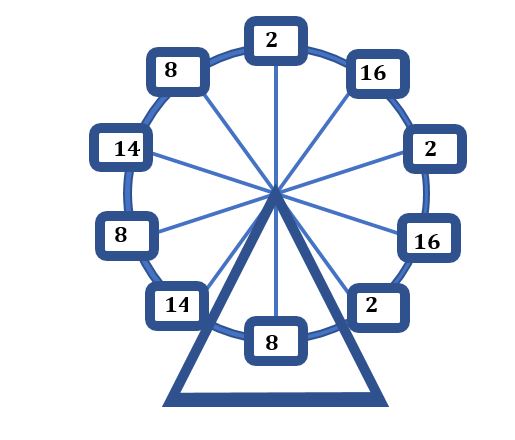
এভাবে ভিন্ন ভিন্ন মান ধরে বাকি যোগফলগুলোও দেখানো যাবে। বুঝা যাচ্ছে, আমাদের এই সপ্তাহের সমস্যার
বেশ কয়েকটি সমাধান আছে।
অনেকেই আমাদের কাছে এই সমস্যাটির সমাধান পাঠিয়েছেন। তবে, সম্পূর্ণ সমাধান কেউ করতে পারেন নি। বেশিরভাগ সমাধানে আংশিক উত্তর এসেছে, এজন্য, সাপ্তাহিক সমস্যা-০৬ এ কাউকে বিজয়ী ঘোষণা করা হচ্ছে না!
যারা উত্তর পাঠিয়েছেন, সবাইকে অভিনন্দন। আশা করি আপনাদের সমস্যা সমাধানের এই যাত্রা অব্যাহত থাকবে। সবার সেকেন্ড ডিফারেন্সিয়াল নেগেটিভ হোক!
(আমাদের অন্যান্য গাণিতিক সমস্যা দেখতে এই লিঙ্কে ক্লিক করুন।)