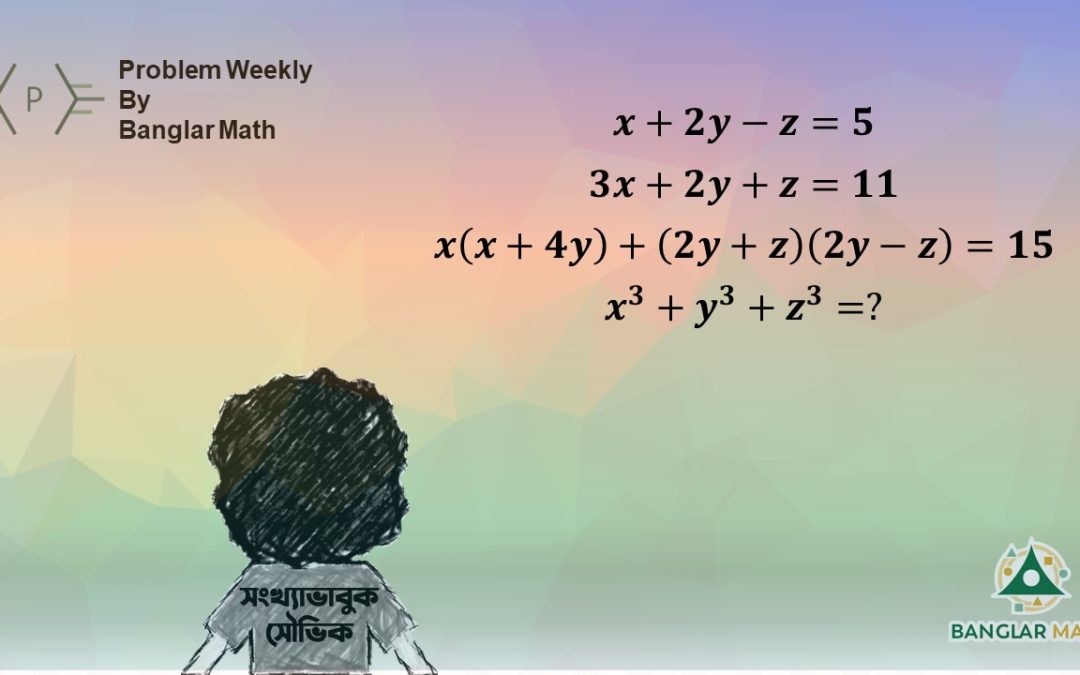সাপ্তাহিক সমস্যা-২৭: সংখ্যাভাবুক সৌভিক সম্প্রতি বীজগণিতের বিভিন্ন সূত্র, নানান রকমের সমীকরণ, এবং সেগুলো কিভাবে সমাধান করা যায় সে সম্পর্কে জানতে পেরেছে। এখন সে অবসর সময়ে বীজগণিতের বিভিন্ন সমীকরণ সমাধান করার চেষ্টা করে। সৌভিকের বন্ধু জ্যামিতিক জামি সৌভিককে একটি তিন চলকের সমীকরণ সমাধান করতে দিলো। সমস্যাটি এরকম:
x + 2y – z = 5
3x + 2y + z = 11
x(x+4y) + (2y+z)(2y-z) = 15
x^3 + y^3 + z^3 = ?
(এখানে x, y এবং z তিনটি পূর্ণসংখ্যা)
সৌভিক অনেকক্ষণ ধরে এটা সমাধান করার চেষ্টা করলো। সৌভিক সমীকরণ সমাধানের জন্য যা যা শিখেছিলো, যেমন- অপনয়ন পদ্ধতি বা প্রতিস্থাপন পদ্ধতি ,সেগুলো প্রয়োগ করে সমাধান করার চেষ্টা করলো। তোমরা কি কোনভাবে সৌভিককে সাহায্য করতে পারবে?
Problem Weekly-27: Number-lover Souvik has recently learned about algebra formulas, different types of equations, and how to solve those things. Now, he tries to solve various problems related to equations in his leisure time. Souvik’s friend Geometric Jami asked Souvik to solve a three-variable equation. The problem is like this –
x + 2y – z = 5
3x + 2y + z = 11
x(x+4y) + (2y+z)(2y-z) = 15
x^3 + y^3 + z^3 = ?
(Here, x, y, and z are three integers.)
Sauvik has tried for a long time to solve this problem. He has applied the concepts that he learned previously such as the elimination or substitution method of solving equations. Can you help Souvik to solve this problem?
সমাধান: প্রদত্ত তিনটি সমীরকণ এরকম-
x + 2y – z = 5 …..(i)
3x + 2y + z = 11 …..(ii)
x(x+4y) + (2y+z)(2y-z) = 15 …..(iii)
এবার সমীকরণ (i) এবং সমীকরণ (ii) যোগ করে পাই,
x + 2y – z + 3x + 2y + z = 11 + 5
বা, 4x + 4y = 16
বা, x + y = 4
বা, y = 4 – x …..(iv)
সমীকরণ (i) থেকে আমরা পাই,
x + 2y – z = 5
বা, 2y – z = 5 – x …..(v)
সমীকরণ (ii) থেকে আমরা পাই,
3x + 2y + z = 11
বা, 2y + z = 11 – 3x …..(vii)
এখন সমীকরণ (iii) এ সবগুলো মান বসিয়ে পাই,
x(x+4y) + (2y+z)(2y-z) = 15
বা, x (x + 4 [4 – x]) + (5 – x) (11 – 3x) = 15
বা, x (x + 16 – 4x) + (5 – x) (11 – 3x) = 15
বা, x (16 – 3x) + (5 – x) (11 – 3x) = 15
বা, 16x – 3x2 + 55 – 15x – 11x + 3x2 = 15
বা, 16x – 26x + 40 = 0
বা, x= 4
তাহলে, x= 4 সমীকরণ (iv) এ বসিয়ে পাই,
y = 4 – x
বা, y = 4 – 4
বা, y = 0
একইভাবে, সমীকরণ (i) এ x= 4 এবং y = 0 বসিয়ে পাই,
x + 2y – z = 5
বা, z = x + 2y – 5
বা, z = 4 + 2 × 0 – 5
বা, z = -1
এবার তাহলে অবশিষ্ট বীজগাণিতিক রাশিটির মান বের করে ফেলি-
x^3 + y^3 + z^3
= 4^3 + 0^3 + (-1)^3
= 64 – 1
= 63
সুতরাং, 63 হচ্ছে আমাদের সাপ্তাহিক সমস্যা-২৭ এর উত্তর!
অনেকেই আমাদের কাছে এই গাণিতিক সমস্যাটির সমাধান পাঠিয়েছে, সবার স্বতঃস্ফূর্ত অংশগ্রহণ আমাদের অভিভূত করেছে। তবে আমরা ৪ জনের সঠিক উত্তর পেয়েছি, তাই সাপ্তাহিক সমস্যা-২৭ এ বিজয়ী চারজন!

ছবি: সাপ্তাহিক সমস্যা-২৭ এর বিজয়ী তালিকা
যারা সমস্যাটির সমাধান করার চেষ্টা করেছো, সবাইকে অভিনন্দন। আশা করি তোমাদের সমস্যা সমাধানের এই চেষ্টা অব্যাহত থাকবে। তোমাদের সবার সেকেন্ড ডিফারেন্সিয়াল নেগেটিভ হোক!
(আমাদের অন্যান্য গাণিতিক সমস্যা দেখতে এই লিঙ্কে ক্লিক করুন।)