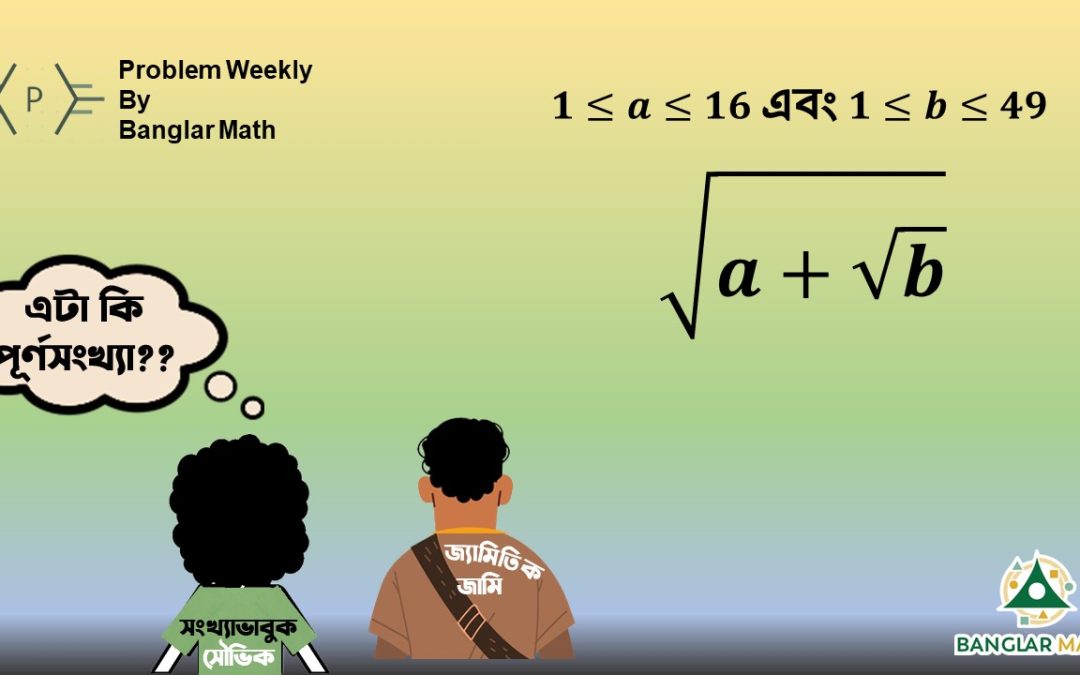সাপ্তাহিক সমস্যা-০৮: সংখ্যা ভাবুক সৌভিক তার বন্ধু জ্যামিতিক জামিকে বিভিন্ন সংখ্যার বর্গ এবং বর্গমূল কিভাবে বের করা যায় সেটি শিখাচ্ছে। কোন একটি সংখ্যাকে ঐ সংখ্যা দিয়েই একবার গুণ করা হলে প্রাপ্ত সংখ্যাকে আমরা বর্গ সংখ্যা বলি।যেমন: 3 × 3 = 9, 5 × 5 = 25 ইত্যাদি। আবার, একই ধারণা দিয়ে কিন্তু বর্গমূলও বের করা যায়। যেমন: √25 = 5, √9 = 3 । কিন্তু খেয়াল রেখো, √26 বা √30 কিন্তু পূর্ণসংখ্যা না! এসব শেখানোর পর সৌভিক জামিকে একটি মজার গাণিতিক সমস্যা দিলো সমাধান করার জন্য। সমস্যাটি ছিলো এরকম:
যদি 1 ≤ a ≤16 এবং 1 ≤ b ≤49 হয়, তাহলে কতগুলো a ও b এর মানের জন্য √(a + √b) এই রাশিটির মান পূর্ণসংখ্যা হবে?
জামি কিছুক্ষণ চেষ্টা করে 10টি সম্ভাব্য উত্তর বের করলো। তোমরা কি বলতে পারবে, জামির উত্তর ঠিক আছে কি না?
Problem Weekly-08: Number-lover Souvik is teaching his friend Geometric Jami how to find the square and square root of different numbers. If a number is multiplied by the same number once, we call it a square number. Like, 3 × 3 = 9, 5 × 5 = 25.
Again, the square root can be derived with the same idea such as √25 = 5, √9 = 3. Note that √26 or √30 are not integers!
After discussing this topic, Souvik gives Jami an interesting problem to find a solution to. The Problem is like that:
If 1 ≤ a ≤16 and 1 ≤ b ≤49, then how many ordered pairs of integer (a, b) are given that the values of √(a + √b) are an integer?
Jami is trying for a while to find out 10 possible answers. Well, can you tell if Jami’s answer is correct or not?
সমাধান: √(a + √b) এর মান তখনই পূর্ণসংখ্যা হবে যখন a + √b এর মান পূর্ণবর্গ সংখ্যা হবে।
যেহেতু a ও b এর অনেকগুলো মান সম্ভব, কাজেই আমাদের দেখতে হবে কোন কোন a ও b এর মানের জন্য a + √b একটি পূর্ণবর্গ সংখ্যা হয়।
প্রশ্নমতে, 1 ≤ b ≤49, তাই √b এর মান হতে পারে শুধুমাত্র 1, 2, 3, 4, 5, 6 এবং 7 (আমরা কিভাবে নিশ্চিত হলাম? ভেবে দেখো তো!)
আচ্ছা, আমরা বর্গসংখ্যার একটা ছক তৈরি করে সম্ভাব্য সমাধান খুঁজে বের করার চেষ্টা করি:
|
a এর মান |
b এর মান |
√b এর মান |
a + √b এর মান |
√(a + √b) এর মান |
|
1 |
9 |
3 |
4 |
2 |
|
2 |
4 |
2 |
4 |
2 |
|
2 |
49 |
7 |
9 |
3 |
|
3 |
1 |
1 |
4 |
2 |
|
3 |
36 |
6 |
9 |
3 |
|
4 |
25 |
5 |
9 |
3 |
|
5 |
16 |
4 |
9 |
3 |
|
6 |
9 |
3 |
9 |
3 |
|
7 |
4 |
2 |
9 |
3 |
|
8 |
1 |
1 |
9 |
3 |
|
9 |
49 |
7 |
16 |
4 |
|
10 |
36 |
6 |
16 |
4 |
|
11 |
25 |
5 |
16 |
4 |
|
12 |
16 |
4 |
16 |
4 |
|
13 |
9 |
3 |
16 |
4 |
|
14 |
4 |
2 |
16 |
4 |
|
15 |
1 |
1 |
16 |
4 |
তাহলে সবমিলিয়ে মোট ভিন্ন ভিন্ন 17 টি a এবং b এর মান পাওয়া গিয়েছে যাদের জন্য √(a + √b) এর মান একটি পূর্ণসংখ্যা হবে। অর্থাৎ, জামির উত্তর ভুল ছিলো!
অনেকেই আমাদের কাছে এই সমস্যাটির সমাধান পাঠিয়েছেন, আপনাদের স্বতঃস্ফূর্ত অংশগ্রহণ আমাদের অভিভূত করেছে। মোট ৯ জনের সঠিক উত্তর পেয়েছি। তাই সাপ্তাহিক সমস্যা-০৮ এ আমাদের মোট বিজয়ী ৯ জন।
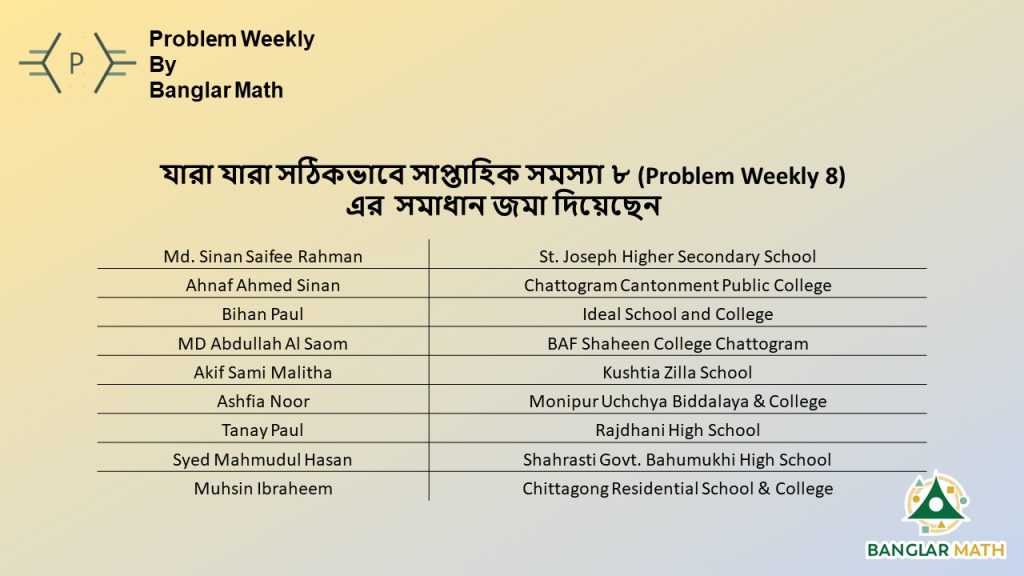
যারা উত্তর পাঠিয়েছেন, সবাইকে অভিনন্দন। আশা করি আপনাদের সমস্যা সমাধানের এই যাত্রা অব্যাহত থাকবে।
সবার সেকেন্ড ডিফারেন্সিয়াল নেগেটিভ হোক!
(আমাদের অন্যান্য গাণিতিক সমস্যা দেখতে এই লিঙ্কে ক্লিক করুন।)