“Sire, there is no royal road to geometry”
শুরু করছি ইউক্লিডের একটি বিখ্যাত্য উক্তি দিয়ে। উক্তিটির ইতিহাসটাও চমৎকার। একবার রাজা প্রথম টলেমি ইউক্লিডকে জিজ্ঞেস করেছিলেন, ‘এলিমেন্টস ছাড়া জ্যামিতি শেখার সহজ কোনো পথ আছে কি?’
তখন ইউক্লিড তার সেই বিখ্যাত উক্তিটি করেন, যার বাংলা অনুবাদটি হচ্ছে কিছুটা এরকম-
“জ্যামিতি শেখার কোনো রাজকীয় পথ নেই”
যদিও আসলে এখানে “Royal Road” বলতে শর্টকার্টের কথা বোঝানো হয়। ইতিহাসের পাতা থেকে আমরা দেখতে পাই পারস্য রাজা Darius বা Darius the Great তার বিশাল সামাজ্যে শর্টকাটে দ্রুত যোগাযোগ ব্যাবস্থা স্থাপনের লক্ষে “The Royal Road” টি তৈরী করেছিলেন।
জ্যামিতির কথা বলতে শুরু করলে সবার আগে যে নামটি মাথায় আসবে সেটি হলো বিখ্যাত গ্রিক গণিতজ্ঞ ইউক্লিড। যার একটি বিখ্যাত্য গ্রন্থ হলো “এলিমেন্টস”। এটি জ্যামিতির জন্য বিখ্যাত হলেও এতে সংখ্যাতত্ত্বের অনেকগুলো বিষয় যেমন: পারফেক্ট নাম্বার ও মার্জেন প্রাইমের মধ্যকার সম্পর্ক এবং গরিষ্ঠ সাধারণ গুণনীয়ক বের করার ইউক্লিডীয় এলগরিদম বর্ণনা করা আছে। ইউক্লিড খ্রিস্টপূর্ব ৩য় শতকের গণিতবিদ ছিলেন। তিনি বুঝতে পারেন যে, তার সময়কার বিভিন্ন জ্যামিতিক উপপাদ্যগুলিকে খুবই অল্প সংখ্যক স্বতঃসিদ্ধের সাহায্যে ব্যাখ্যা করা সম্ভব। মাত্র পাঁচটি স্বতঃসিদ্ধ থেকে সকল সমতলীয় বা ইউক্লিডীয় জিওমেট্রি ব্যাখ্যা করা যায়। সেগুলো হলো─
১) যেকোন দুইটি প্রদত্ত বিন্দুর মধ্য দিয়ে শুধুমাত্র একটি সরলরেখা আঁকা সম্ভব।
২) কোন সরলরেখাকে অসীম পর্যন্ত প্রসারিত করা যায় কিংবা যেকোন বিন্দুতে সীমাবদ্ধ করা যায়।
৩) যেকোন বিন্দুকে কেন্দ্র ধরে ও যেকোন ব্যাসার্ধ (বৃত্তের যেকোন বিন্দু থেকে কেন্দ্রের দূরত্ব) নিয়ে একটিমাত্র বৃত্ত আঁকা সম্ভব।
৪) সব সমকোণ সবসময় সমান।
৫) একটি প্রদত্ত সরলরেখার বহিঃস্থ একটি প্রদত্ত বিন্দু দিয়ে প্রথম সরলরেখার সমান্তরাল কেবলমাত্র একটি সরলরেখা আঁকা সম্ভব।
জ্যামিতির সবচেয়ে চমৎকার জিনিস হলো এটা দৃশ্যমান। আমরা চোখের সামনে ছবি এঁকে বুঝতে পারি, প্রমাণ করতে পারি, খেয়াল খুশি মত প্রয়োজনীয় চিত্র আঁকতে পারি। তবে একটি কথা মাথায় রাখতে হবে, প্রমাণ করতে হবে যুক্তি দিয়ে, স্বীকার্য দিয়ে, উপপাদ্য দিয়ে। এখানে নিজের মনে হলো তাই এটাই হতে হবে, এরকম কিছু কাজ করে না। অথবা, অমুক এটা বলছে বলে এই রেখাটা সমদ্বিখন্ডক হবে─ এরকম কথার কোনো ভিত্তি নেই। এবং প্রমাণ করতে হবে ধাপে ধাপে, যে কোন প্রমাণের প্রতিটি ধাপকে হয় কোন স্বতঃসিদ্ধ অথবা পূর্ব-প্রমাণিত কোন উপপাদ্য দিয়ে সমর্থিত হতে হয়। সঠিকভাবে জ্যামিতির চিত্র আঁকতে পারলে তোমার চোখের সামনে অনেক কিছু দৃশ্যমান হয়ে উঠবে। যেখান থেকে তুমি খুঁজে পেতে পারো তোমার কাঙ্ক্ষিত তথ্য, যা প্রমাণের বিভিন্ন ধাপের জন্য গুরুত্বপূর্ণ।
আমাদের ষষ্ঠ শ্রেণি থেকে নবম শ্রেণির পাঠ্যবইয়ে ইউক্লিডীয় জ্যামিতি খুব সুন্দর করে পর্যায়ক্রমে উল্লেখ করা আছে। আছে অনুশীলনীর জন্য অনেকগুলো সমস্যা। যে কেউ যদি বুঝে বুঝে সময় নিয়ে এই সমস্যাগুলো সমাধানের চর্চা করে, তাহলে এই বিষয়ে প্রাথমিক ভিত্তি তৈরী হয়ে যাবে। এরপর, জ্যামিতির অন্য যে কোন বই পড়তে কিংবা তাত্ত্বিক বিষয় বুঝতে খুব একটা সমস্যা হবে না।
জ্যামিতির সাহায্যে গণিতের আরো অনেক বিষয়ের গাণিতিক প্রমাণ আমরা সহজে বুঝতে পারি। আমরা বীজগণিতের প্রাথমিক ধারণা লাভ করার সময় বন্ধনীর ব্যবহার, একাধিক চলকের মধ্যে যোগ-বিয়োগ-গুণ-ভাগ ইত্যাদি কিভাবে হয় সেটা শিখে থাকি। আসলে (a + b) 2 = a 2 + 2ab + b 2 এটা কিভাবে হলো সেটা জ্যামিতিক চিত্র দিয়ে সহজে বোঝানো যায়।
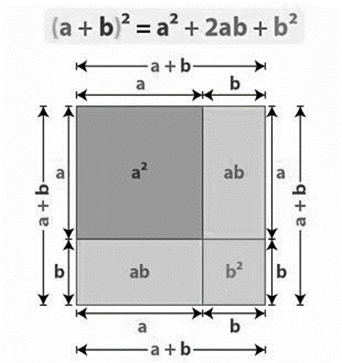
ছবি: বীজগণিতের (a + b) 2 সূত্রের সচিত্র জ্যামিতিক ব্যাখ্যা
আবার, আমরা সবাই সংখ্যা চেনার পর থেকে কিন্তু সংখ্যারেখার সাথে পরিচিতি হই। সংখ্যারেখায় সকল বাস্তব সংখ্যাকে কিন্তু চিহ্নিত করা যায়। পূর্ণ সংখ্যাগুলো আমরা সহজেই দেখাতে পারি সংখ্যারেখাতে । আচ্ছা, তোমরা কি অমূলদ সংখ্যা বা √2 সংখ্যাটিকে সংখ্যারেখায় দেখাতে পারবে? জ্যামিতির ধারণা দিয়ে কিন্তু চাইলেই √2 সহ আরো অনেক অমুলদ সংখ্যাকে সংখ্যারেখায় দেখানো সম্ভব। এখন একটু চিন্তা করো, কেন আমি সকল অমূলদ সংখ্যা না বলে আরো অনেক অমূলদ সংখ্যা বলেছি? কেন?
এছাড়া, তোমরা যারা অরিগ্যামি, ট্যানগ্রাম ইত্যাদির নাম শুনেছো তারা হয়তো বুঝতে পারছো এগুলোর পেছনে জ্যামিতির অনেক ধারণা লুকিয়ে আছে। এগুলো নিয়ে অনেক ঐতিহাসিক গল্প আছে, খুঁজে দেখতে পারো। একটা সমস্যা দিচ্ছি, সমাধান করার চেষ্টা করতে পারো:
ট্যানগ্রামে আসলে একটি বর্গাকার কাগজকে বিভিন্ন উপায়ে সাতটি টুকরো করা হয়। সাতটি টুকরোর মধ্যে পাঁচটি ত্রিভুজ, একটি সামান্তরিক এবং একটি বর্গ পাওয়া যায়। একটু চিন্তা করে বলো তো, ছোট বর্গটির ক্ষেত্রফল মূল কাগজের কত অংশ হতে পারে?

ছবি: ট্যানগ্রাম
আসলে জ্যামিতি কিন্তু এখন শুধুমাত্র ভূমির পরিমাপের মধ্যেই সীমাবদ্ধ না। এটি যুক্তি এবং প্রমাণের একটি চমৎকার স্বতঃস্ফূর্ত উপস্থাপন। জ্যামিতি হলো একটি ছোট জানালা যেটির সাহায্যে বীজগণিতের বৈশিষ্ট্যগুলো প্রকাশিত হয়, যার মাধ্যমে তুমি ‘কেন’ এর উত্তর আবিষ্কারের আনন্দে বিভোর হয়ে যাবে।
“Geometry is the most complete science” — David Hilbert
এটাই জ্যামিতি!!
(এ ধরণের আর্টিকেল আরো পড়তে চাইলে এখানে ক্লিক করুন।)
লেখক: আশরাফুল-আল-শাকুর (ইমেইল: bm.ashrafulshakur@gmail.com)

